To demonstrate how you can use EpiModel with data inputs from network census and egocentrically sampled designs we will return to the built-in adolescent friendship network data “faux.mesa.high” (“Mesa”) from the ergm package.

Mesa is a network census based on one of the “saturation” sample schools from the Add Health study (wave 1). Questionnaires were completed by all of the students from the 7th-12th grades, and they were asked to nominate up to 5 close male and 5 close female friends from a roster that included the names of all students in their school, and a code for friends who were not enrolled in the school. More information on the study design can be found here. The network included in the ergm package is a simplified and anonymized version of the original data, using a model-based simulation of the mutual in-school nominations only, so it is an undirected network. More information on the details and construction of the simulated dataset can be found by typing ?faux.mesa.high.

This is a static network, and the Add Health study did not include questions about partnership duration. We will use a hypothetical average friendship length to parameterize the duration.

Epimodel’s network methods have the flexibility to be entirely driven by a single dataset (when all necessary data have been collected), to combine data from different studies, or to introduce parameters for exploring “what-if” scenarios.

Note

Download the R script to follow along with this tutorial here.

Let’s start by loading the EpiModel package. Optionally, also install the Rglpk package to use the preferred solver during estimation.

Code 
library(EpiModel)
#install.packages("Rglpk")
library(ndtv)

29.1 Using Network Census Data

29.1.1 Load the data

We’ll load it, and look at the summary. Note that the class of the built-in Mesa data object is network. If you have data from a network census study design, the methods for creating network objects from your data can be found in one of the Statnet intro workshops.

Code 
data("faux.mesa.high")
mesa <- faux.mesa.high
class(mesa)
[1] "network"
Code 
mesa
 Network attributes:
  vertices = 205 
  directed = FALSE 
  hyper = FALSE 
  loops = FALSE 
  multiple = FALSE 
  bipartite = FALSE 
  total edges= 203 
    missing edges= 0 
    non-missing edges= 203 

 Vertex attribute names: 
    Grade Race Sex 

No edge attributes

29.1.2 Explore attribute effects

We’ll focus on two of the attributes here – Grade and Sex – and use some basic R utilities to explore whether these are associated with heterogeneity in behavior (degree) and network structure (mixing patterns).

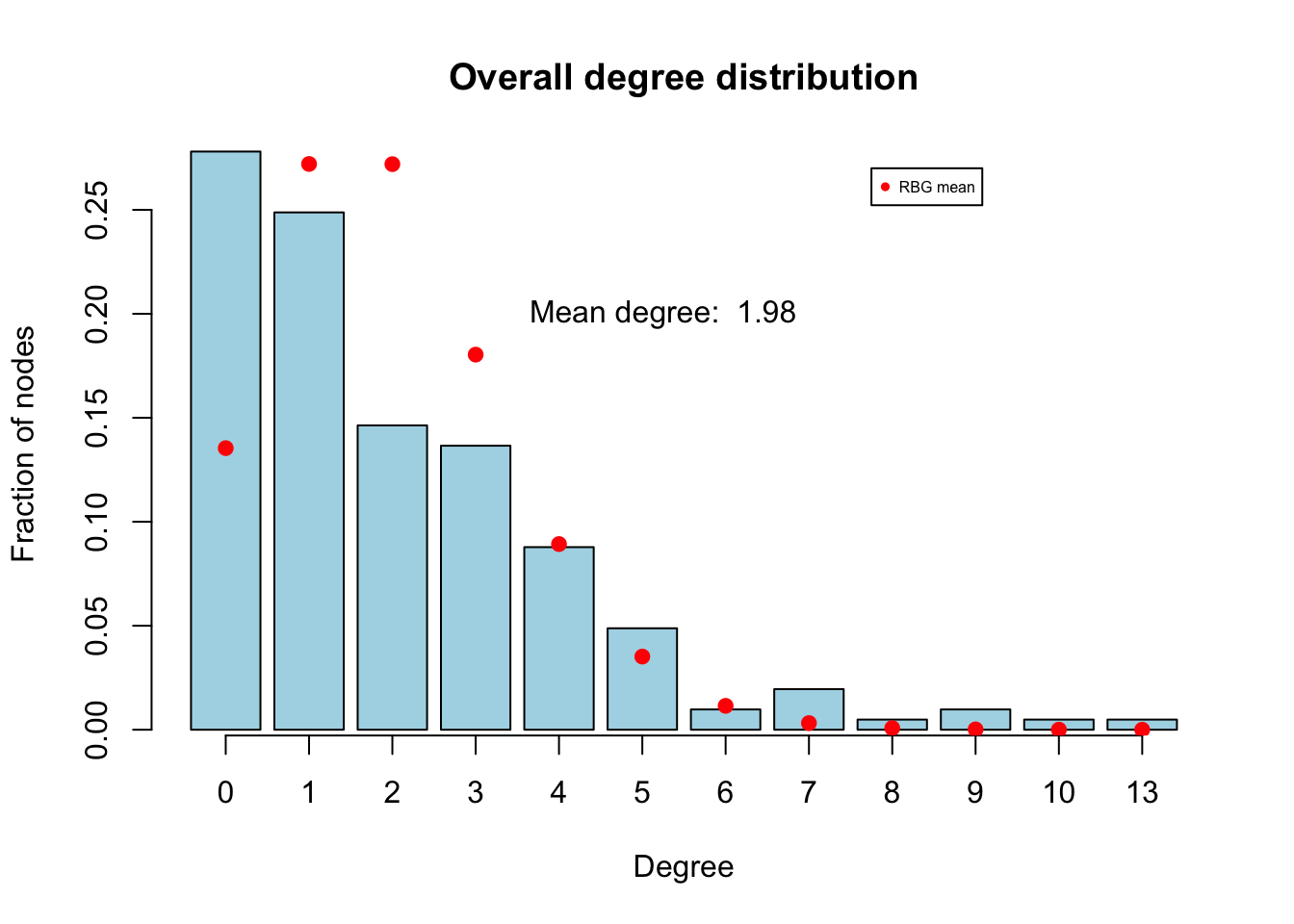
Degree distributions:

Code 
fill.col <- RColorBrewer::brewer.pal(8, "Set2") # 8 colors

# Overall
barplot(degreedist(mesa)/network.size(mesa),  xaxt = "n",
        main = "Overall degree distribution", 
        xlab = "Degree", ylab = "Fraction of nodes",
        col = "lightblue")
 degree0  degree1  degree2  degree3  degree4  degree5  degree6  degree7 
      57       51       30       28       18       10        2        4 
 degree8  degree9 degree10 degree13 
       1        2        1        1
Code 
degs <- gsub("degree", "", names(degreedist(mesa)))
 degree0  degree1  degree2  degree3  degree4  degree5  degree6  degree7 
      57       51       30       28       18       10        2        4 
 degree8  degree9 degree10 degree13 
       1        2        1        1
Code 
pos <- barplot(degreedist(mesa), plot=F)
 degree0  degree1  degree2  degree3  degree4  degree5  degree6  degree7 
      57       51       30       28       18       10        2        4 
 degree8  degree9 degree10 degree13 
       1        2        1        1
Code 
axis(1, at = pos, labels = degs)
points(x=pos, y=dbinom(c(0:10, 13), size=205, prob=1.98/204), col="red", pch=19)
text(7, 0.2, paste("Mean degree: ", round(summary(mesa ~ meandeg), 2)))
legend(10, 0.27, pch=19, col="red", "RBG mean", cex=.5)

Code 
par(mfrow=c(1,2))
# by Grade

barplot(summary(mesa ~ nodefactor("Grade", levels=T)) / table(mesa %v% "Grade"), 
        horiz = T, 
        yaxt = "n", col = fill.col,
        main = "Mean degree by Grade", xlab = "Mean degree", ylab = "Grade")
grades <- c(7:12)
pos <- barplot(summary(mesa ~ meandeg:nodefactor("Grade", levels=TRUE)), 
               horiz = T, plot=F)
axis(2, at = pos, labels = grades)

# by sex

barplot(summary(mesa ~ nodefactor("Sex", levels=T)) / table(mesa %v% "Sex"), horiz = T, 
        yaxt = "n", col=fill.col[7:8],
        main = "Mean degree by Sex", xlab = "Mean degree", ylab = "Sex")
sex <- c("F", "M")
pos <- barplot(summary(mesa ~ meandeg:nodefactor("Sex", levels=TRUE)), 
               horiz = T, plot=F)
axis(2, at = pos, labels=sex)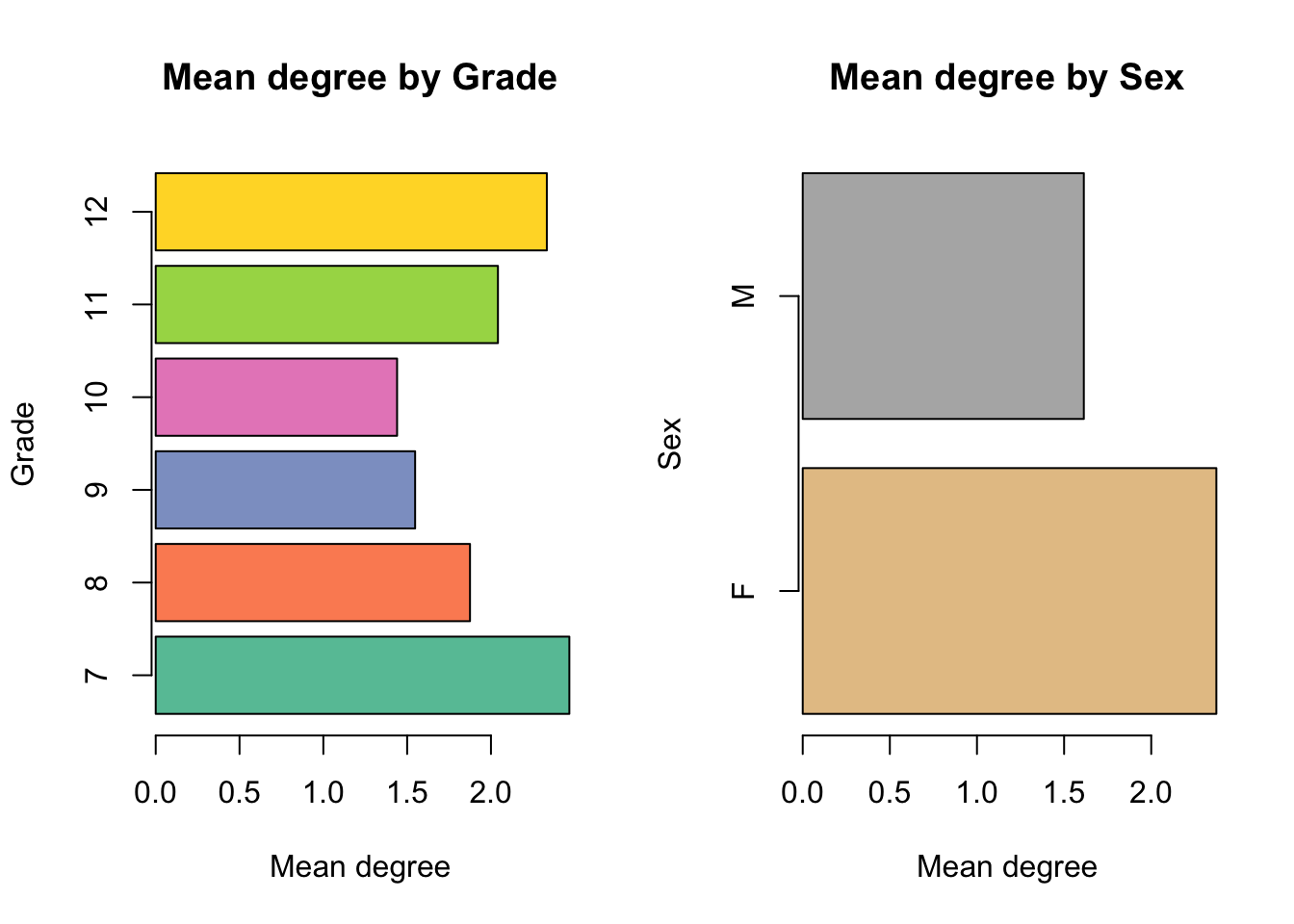

Code 
# Isolates by sex
round(100*(summary(mesa ~ degree(0, by="Sex")) / table(mesa %v% "Sex")), 1)

   F    M 
23.2 32.1

Mixing patterns:

Code 
set.seed(0)
coords <- plot(mesa)
Code 
mixingmatrix(mesa, "Grade")
    7  8  9 10 11 12
7  75  0  0  1  1  1
8   0 33  2  4  2  1
9   0  2 23  7  6  4
10  1  4  7  9  1  5
11  1  2  6  1 17  5
12  1  1  4  5  5  6
Note:  Marginal totals can be misleading for undirected mixing matrices.
Code 
mixingmatrix(mesa, "Sex")
   F  M
F 82 71
M 71 50
Note:  Marginal totals can be misleading for undirected mixing matrices.
Code 
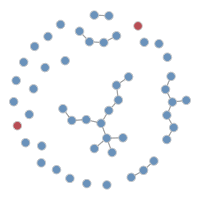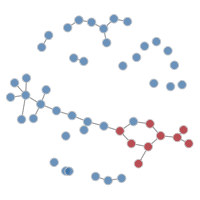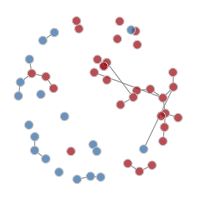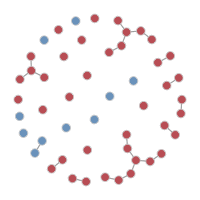
par(mfrow = c(1,2), oma=c(0,0,3,0))

plot(mesa, coord=coords,
     vertex.col='Grade', main="By Grade", cex.main = 1)
legend('bottomleft',fill=7:12,
       legend=paste('Grade',7:12),cex=0.5)

plot(mesa, coord=coords,
     vertex.col='Sex', main="By Sex", cex.main = 1)
legend('bottomleft',fill=1:2,
       legend=paste('Sex',c("F","M")),cex=0.5)

mtext("Mesa friendship network", side=3, outer=T, cex=1.5)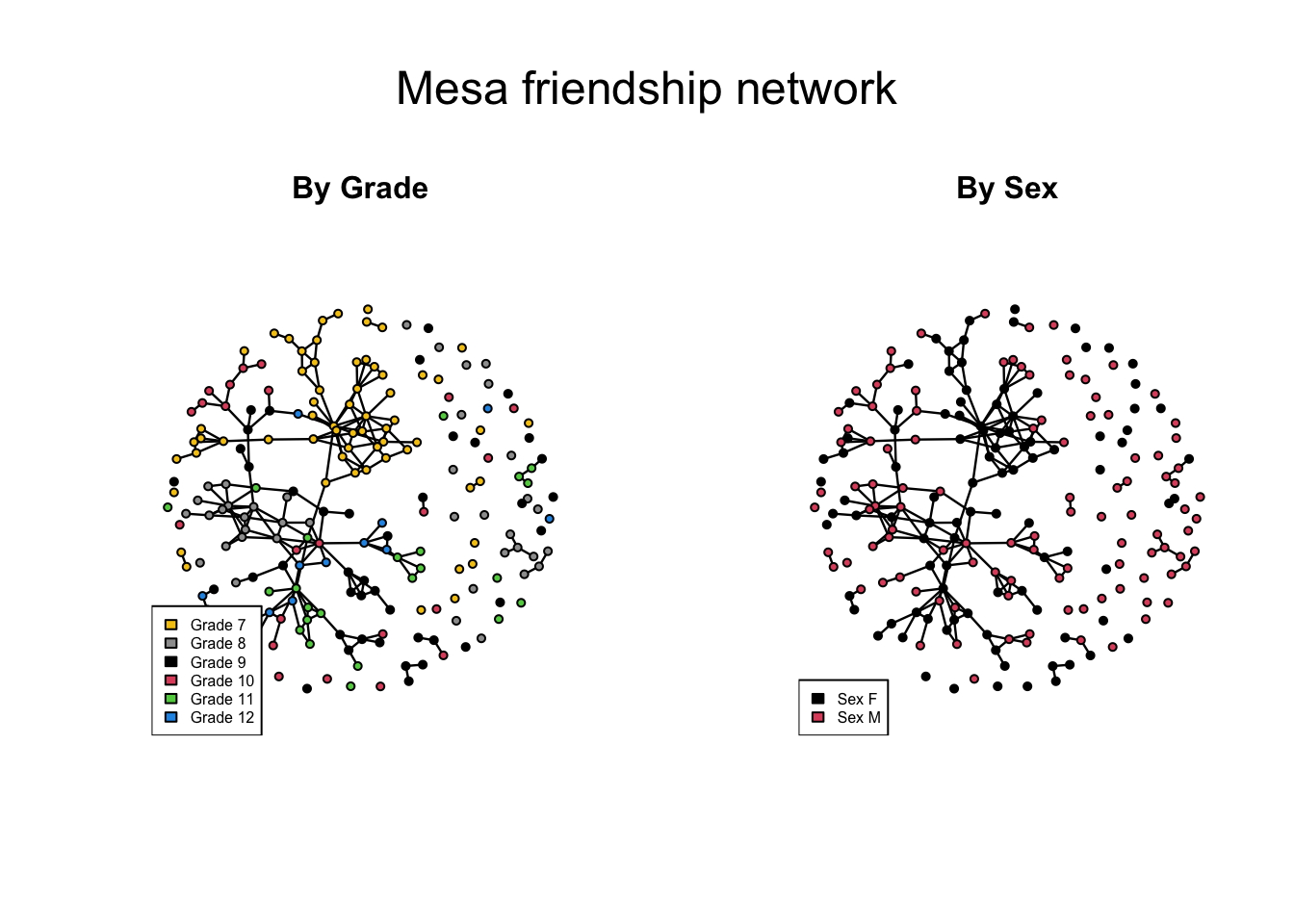

The EDA replicates what we saw in this network using statnetWeb: both the sex and grade attributes influence friendship prevalence and selection, producing a network with some clear heterogeneities in structure.

29.1.3 Specify the model

We explored several models in statnetWeb, but here we want to focus on demonstrating how network data are used in an EpiModel workflow. So we won’t spend time testing and comparing models for the network, but the lab will give you a chance to do some of that.

We are going to fit a specific model for attribute heterogeneities that is (loosely) informed by the EDA above:

  • “main effects” for sex and grade (nodefactor) – to represent the difference in mean degree by levels of each attribute;
  • a mixing term for grade (nodematch) – to represent homophily by grade;
  • a degree(0) term by sex – to represent the differential prevalence of isolates for boys and girls.

29.1.4 Fitting the Network Model

Following the terminology and syntax demonstrated previously, we would like to fit a TERGM where the formula includes terms for overall mean degree (edges), mean degree by grade and sex (nodefactor terms) mixing by grade (a nodematch term), and isolates by sex (having a degree of exactly zero). A total of 11 terms is specified by this model.

Code 
formation <- ~ edges + 
  nodefactor("Grade") + nodematch("Grade") +
  nodefactor("Sex") +   nodematch("Sex") +
  degree(0, by = "Sex")

Since we are using network data input we can use ergm to calculate the summary statistics for these model terms directly from the data using the summary() function. These are the statistics used as the target stats in the fitting process.

Code 
targets <- summary(mesa ~ edges + 
  nodefactor("Grade") + nodematch("Grade") +
  nodefactor("Sex") +   nodematch("Sex") +
  degree(0, by = "Sex"))

targets
              edges  nodefactor.Grade.8  nodefactor.Grade.9 nodefactor.Grade.10 
                203                  75                  65                  36 
nodefactor.Grade.11 nodefactor.Grade.12     nodematch.Grade    nodefactor.Sex.M 
                 49                  28                 163                 171 
      nodematch.Sex          deg0.Sex.F          deg0.Sex.M 
                132                  23                  34

We then fit the TERGM with the above formula and data, adding a hypothetical parameter for the dissolution model that produces a mean relational duration of 60 time steps.

Code 
set.seed(0)
myfit <- netest(mesa,
                formation = formation,
                target.stats = targets,
                coef.diss = dissolution_coefs(~offset(edges), 60))

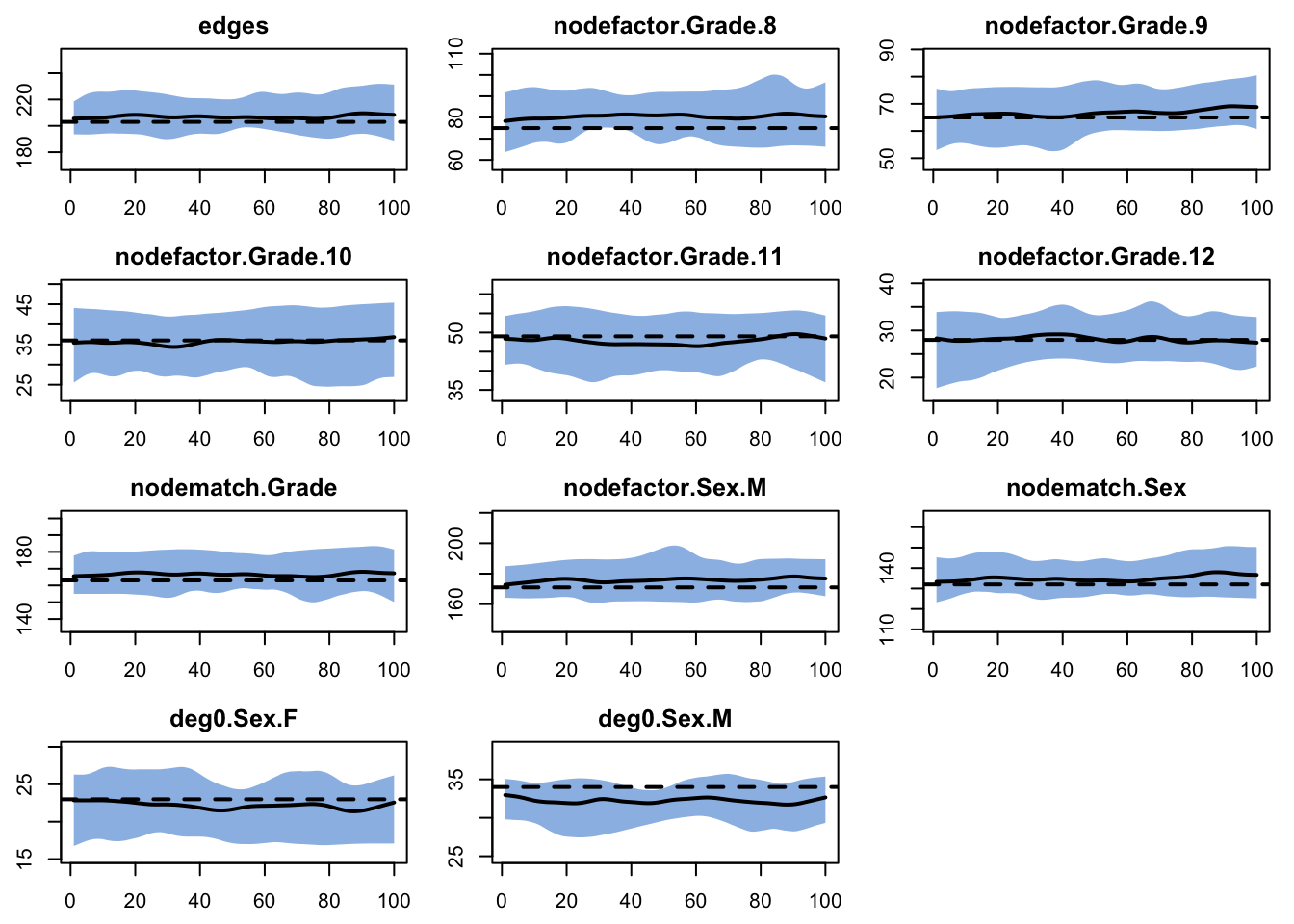
Next, we run fit diagnostics to verify that the target stats are reproduced in expectation.

Code 
mydx <- netdx(myfit, nsims = 25, nsteps = 100, ncores = 5)

plot(mydx)

Note, we can also run dx for network statistics we didn’t include in the model, and this can be a quick way to assess the model GOF to features that were not explicitly represented. Let’s take a look at the observed values of some and compare them to the netstats produced by this model.

Code 
summary(mesa ~ meandeg + gwdegree(.5, fixed=T) + kstar(2) + triangles)
        meandeg gwdeg.fixed.0.5          kstar2        triangle 
       1.980488      199.565738      659.000000       62.000000
Code 
set.seed(1)
mydx <- netdx(myfit, nsims = 25, nsteps = 100, ncores = 5,
              nwstats.formula = ~ meandeg + gwdegree(.5, fixed=T) + 
                kstar(2) + triangles,
              keep.tedgelist = TRUE)

Network Diagnostics
-----------------------
- Simulating 25 networks
- Calculating formation statistics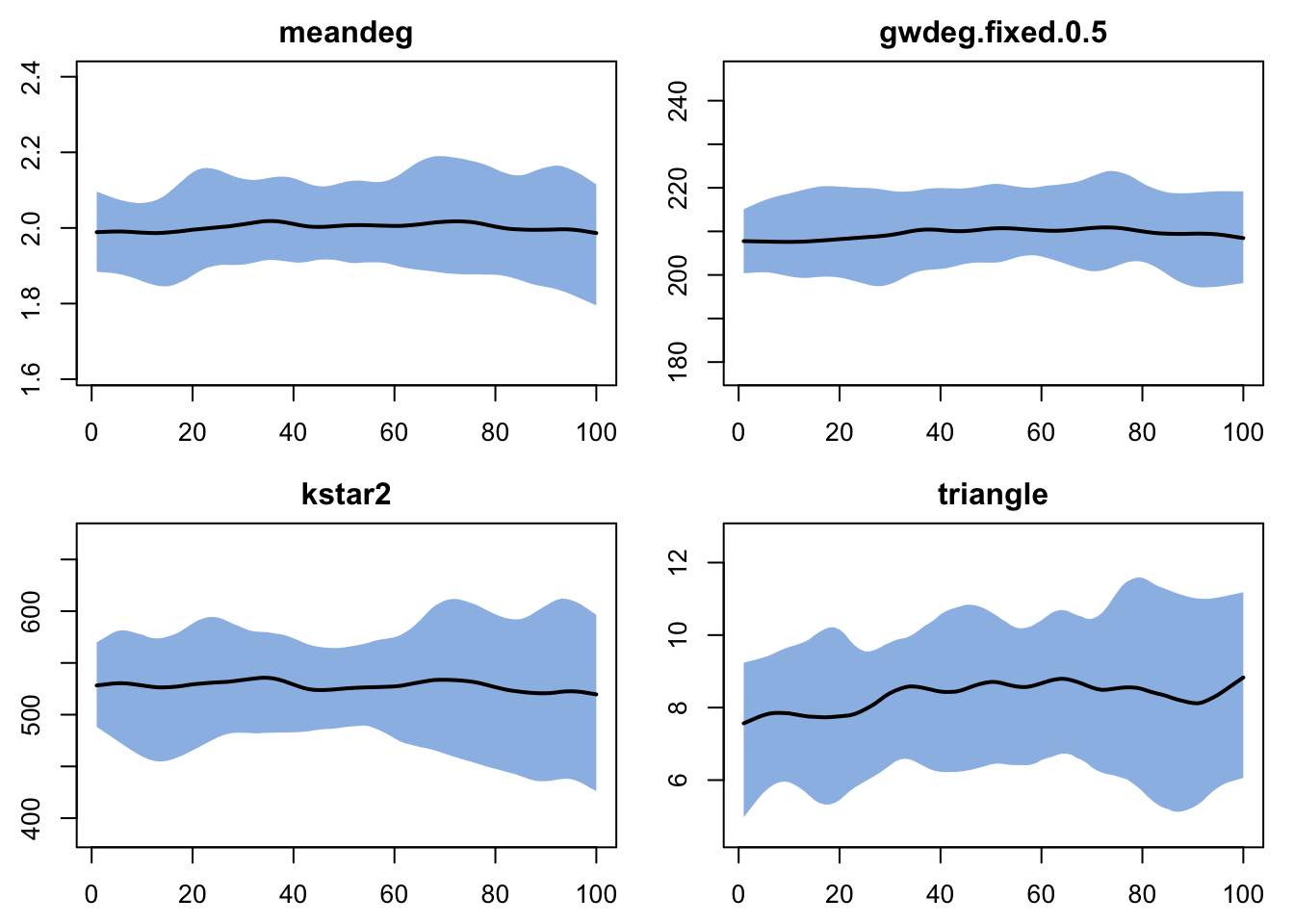
Code 
plot(mydx)

Which of these netstats are reproduced by the model? Which are not?

You can also extract the raw data that goes into producing these numerical summaries and plots to work with them later.

Code 
head(get_nwstats(mydx), 10)
   time sim  meandeg gwdeg.fixed.0.5 kstar2 triangle
1     1   1 1.902439        194.6103    520        9
2     2   1 1.902439        195.2788    514        9
3     3   1 1.921951        194.8129    531       10
4     4   1 1.912195        192.0841    532       11
5     5   1 1.902439        192.0766    520       11
6     6   1 1.921951        192.1490    539       11
7     7   1 1.902439        191.8629    526       11
8     8   1 1.882927        191.1496    514        9
9     9   1 1.912195        192.0039    531        9
10   10   1 1.912195        191.6711    536        9

29.1.5 Epidemic Simulation

To get the epidemic simulation started, we need to set the epidemic model parameters, initial conditions, and control settings (details provided here).

Code 
myparam <- param.net(inf.prob = 0.2,
                     act.rate = 1.8,
                     rec.rate = 0.1)
myinit <- init.net(i.num = 10)

# Here we set which attribute to use for epi stats breakdowns 
# (only one can be specified in base EpiModel) 
# and also which stats we want to monitor

mycontrol <- control.net("SIS", nsteps = 100, nsims = 10,   
                         epi.by = "Grade",
                         nwstats.formula = ~edges + nodematch("Grade") + 
                         degree(0:2, by = "Sex"),
                         verbose = TRUE)

Run the epidemic simulation with netsim.

Code 
set.seed(0)
mySIS <- netsim(myfit, param = myparam, init = myinit, control = mycontrol)

plot(mySIS, formation=T)

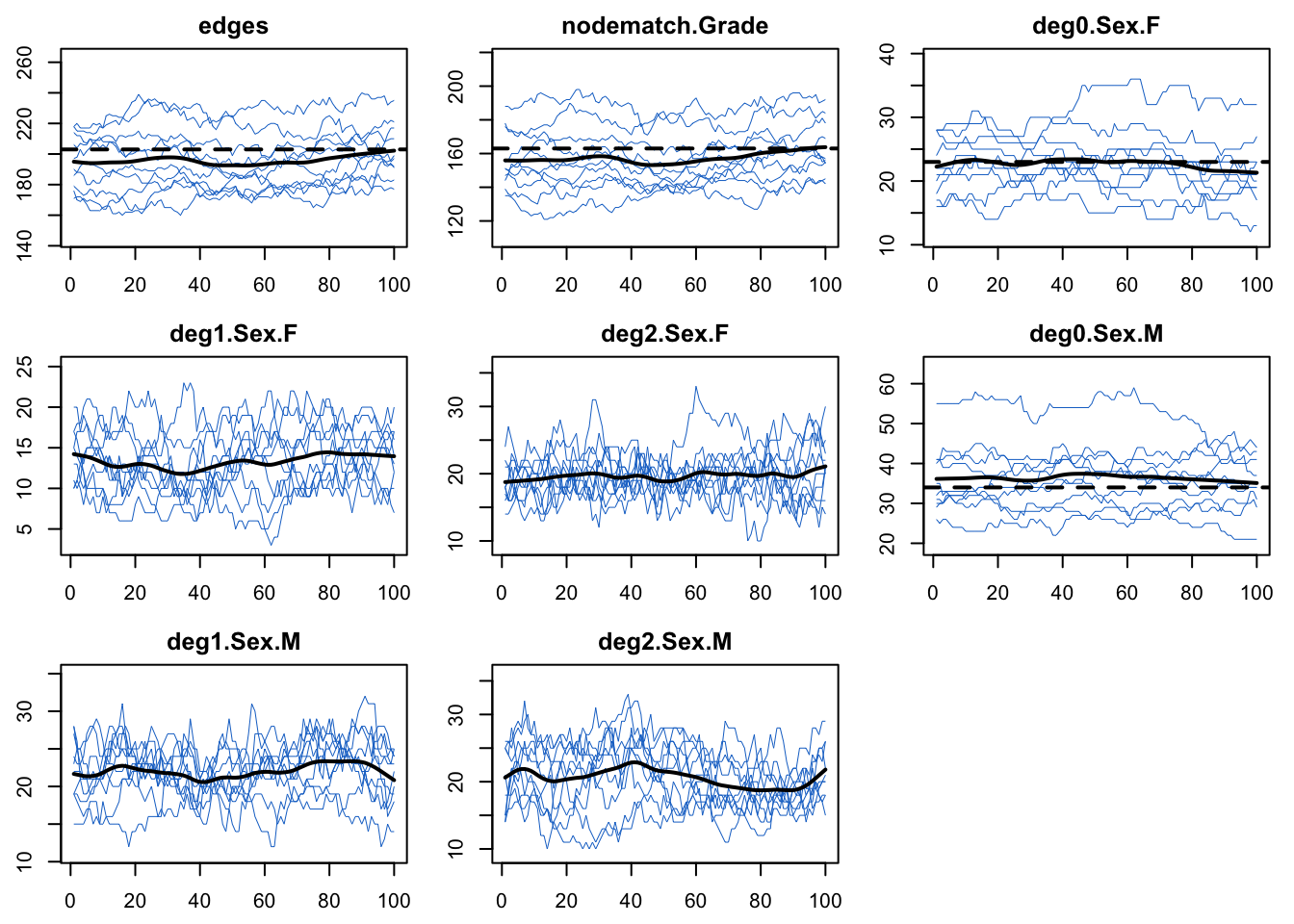
How does prevalence vary by grade? Since the grade sizes are unequal, it’s best to compare rates rather than raw numbers. We construct and plot those below. Note that despite clear degree differences and homophily by grade, and some early prevalence differentials, the prevalence eventually stabilizes at similar levels for all grades. This happens because the transmission probability is relatively high, the network is relatively well connected over time and there are no groups that are completely isolated from the others.

Code 
mySIS <- mutate_epi(mySIS, 
                    prev.7 = i.num.Grade7 / num.Grade7,
                    prev.8 = i.num.Grade8 / num.Grade8,
                    prev.9 = i.num.Grade9 / num.Grade9,
                    prev.10 = i.num.Grade10 / num.Grade10,
                    prev.11 = i.num.Grade11 / num.Grade11,
                    prev.12 = i.num.Grade12 / num.Grade12)

plot(mySIS, y = c("prev.7", "prev.8", "prev.9", "prev.10",
                  "prev.11", "prev.12"), 
     qnts.alpha = 0.2, qnts = 0.5, legend = TRUE)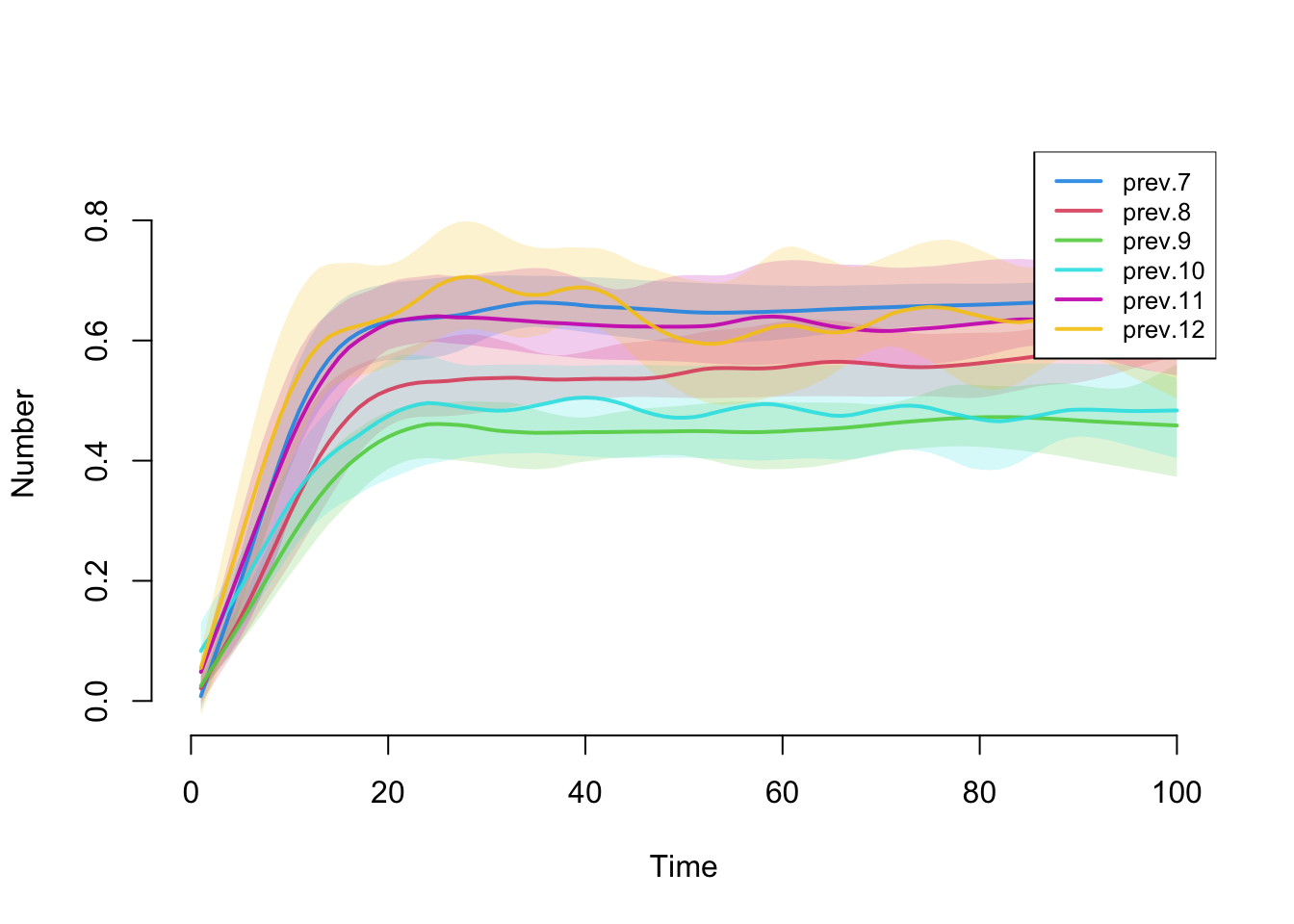

It’s also a good idea to plot the network stats time series from the epidemic simulations to ensure that the epidemic simulations did not have unintended consequences on the network structure.

Code 
plot(mySIS, type = "formation", qnts = FALSE, sim.lines = TRUE)

29.1.6 Dynamic Visualization

The simulation object you created can be passed to the ndtv package for animation, allowing you to see how the infection is moving through the network of students. Recall that the while the network data we started with was a network census, it was a static network. So we passed a hyptothetical average partnership duration to EpiModel for calculating the dissolution model and parameterizing the TERGM. So the network structure is coming from the observed data, and the dynamics of tie formation and dissolution from the hypothetical.

We’ll vizualize the first 20 steps of the epidemic simulation to get a sense of what the network, and the spread, look like.

Code 
myEpiSim <- get_network(mySIS)
myEpiSim <- color_tea(myEpiSim, verbose = FALSE)

slice.par <- list(start = 1, end = 20, interval = 1, 
                  aggregate.dur = 1, rule = "any")
render.par <- list(tween.frames = 10, show.time = FALSE)
plot.par <- list(mar = c(0, 0, 0, 0))

compute.animation(myEpiSim, slice.par = slice.par, verbose = TRUE)
render.d3movie(
  myEpiSim,
  render.par = render.par,
  plot.par = plot.par,
  vertex.cex = 0.9,
  vertex.col = "ndtvcol",
  edge.col = "darkgrey",
  vertex.border = "lightgrey",
  displaylabels = FALSE,
  output.mode = "htmlWidget")

Given what you know about this network, how well do you think this simulated model captures the heterogeneity in friendship structure? Does the animated network seem to have the same structure over time? If not, how would you modify the workflow above to address this?

So that’s the workflow when working with a network census dataset and a hypothetical edge duration parameter. Behind the curtain, this is the breakdown of how the packages are used:

  1. netest()

  • the ergm package calculates the target statistics from the network data and estimates the formation model that you specified for the faux.mesa.high nodeset.

  • the EpiModel package calculates the dissolution coefficient and adjusts the coefficient on the edges term of the formation model to transform it to an incidence rate.

  1. netdx()
  • the tergm package simulates a complete dynamic network over time from the fitted model and keeps a list of the monitored statistics for inspection/plotting
  1. netsim()

  • the tergm package simulates a complete dynamic network over time from the fitted model (as above).

  • the EpiModel package simulates the transmission process over the dynamic network

  1. animation

  • EpiModel extracts the network and colors the nodes by infection status (get_network, color_tea)

  • ndtv animates the colored dynamic network (with compute.animation and render.d3movie)

29.2 Using egocentrically sampled data

Now we will extract the ego networks from Mesa run the same EpiModel simulation using egocentrically sampled data as the input, and show that the results are the same.

29.2.1 Load the ergm.ego package

Code 
library(ergm.ego)

29.2.2 Extract the egocentric data

For this example we will extract an egocentric census – that is, we will pull the egonets for every node in the Mesa network. We do this to highlight the similarities and differences in the data format (rather than the content of the network data) and the downstream impacts.

The object we extract from Mesa is an egor class object (egor is the name of the package that handles egodata), and it’s a list that contains 3 tables: egos (with their attributes), alters (with their attributes and the egoID they are linked to) and aaties (if these are present). The format of the summary information is different than the format used with network objects. For more details about the structure of egor objects and how to work with them please see ?as.egor and the Statnet ergm.ego workshop.

Code 
mesa.ego <- ergm.ego:::as.egor.network(mesa)
class(mesa.ego)
[1] "egor" "list"
Code 
mesa.ego
# EGO data (active): 205 × 4
  .egoID Grade Race  Sex  
*  <int> <dbl> <chr> <chr>
1      1     7 Hisp  F    
2      2     7 Hisp  F    
3      3    11 NatAm M    
4      4     8 Hisp  M    
5      5    10 White F    
# ℹ 200 more rows
# ALTER data: 406 × 5
  .altID .egoID Grade Race  Sex  
*  <int>  <int> <dbl> <chr> <chr>
1    174      1     7 Hisp  F    
2    161      1     7 Hisp  F    
3    151      1     7 Hisp  F    
# ℹ 403 more rows
# AATIE data: 372 × 3
  .egoID .srcID .tgtID
*  <int>  <int>  <int>
1      1    151    127
2      1    127     52
3      1    127     87
# ℹ 369 more rows
Code 
summary(mesa.ego)
205 Egos/ Ego Networks 
406 Alters 
Min. Netsize 1 
Average Netsize 2.74324324324324 
Max. Netsize 13 
Average Density 0.750903163274297 
Alter survey design:
  Maximum nominations: Inf

Let’s verify that the ego attribute distribution is the same as in the Mesa network object.

Code 
table(mesa %v% "Grade", mesa %v% "Sex")
    
      F  M
  7  35 27
  8  15 25
  9  22 20
  10 10 15
  11 10 14
  12  7  5
Code 
table(mesa.ego$ego$Grade, mesa.ego$ego$Sex)
    
      F  M
  7  35 27
  8  15 25
  9  22 20
  10 10 15
  11 10 14
  12  7  5

29.2.3 Explore the data

The simple structure of the egor object makes it relatively easy to conduct EDA using the traditional tools in R, and examples can be found in the Statnet workshop for ergm-ego. We’ll just highlight one nice plotting function built into ergm-ego for looking at degree distributions by attributes, with the BRG distribution overlay.

Code 
degreedist(mesa.ego, by="Sex", brgmod=T,
           main="Mesa degree distribution by Sex")

Code 
degreedist(mesa.ego, by="Grade", brgmod=T,
           main="Mesa degree distribution by Grade")

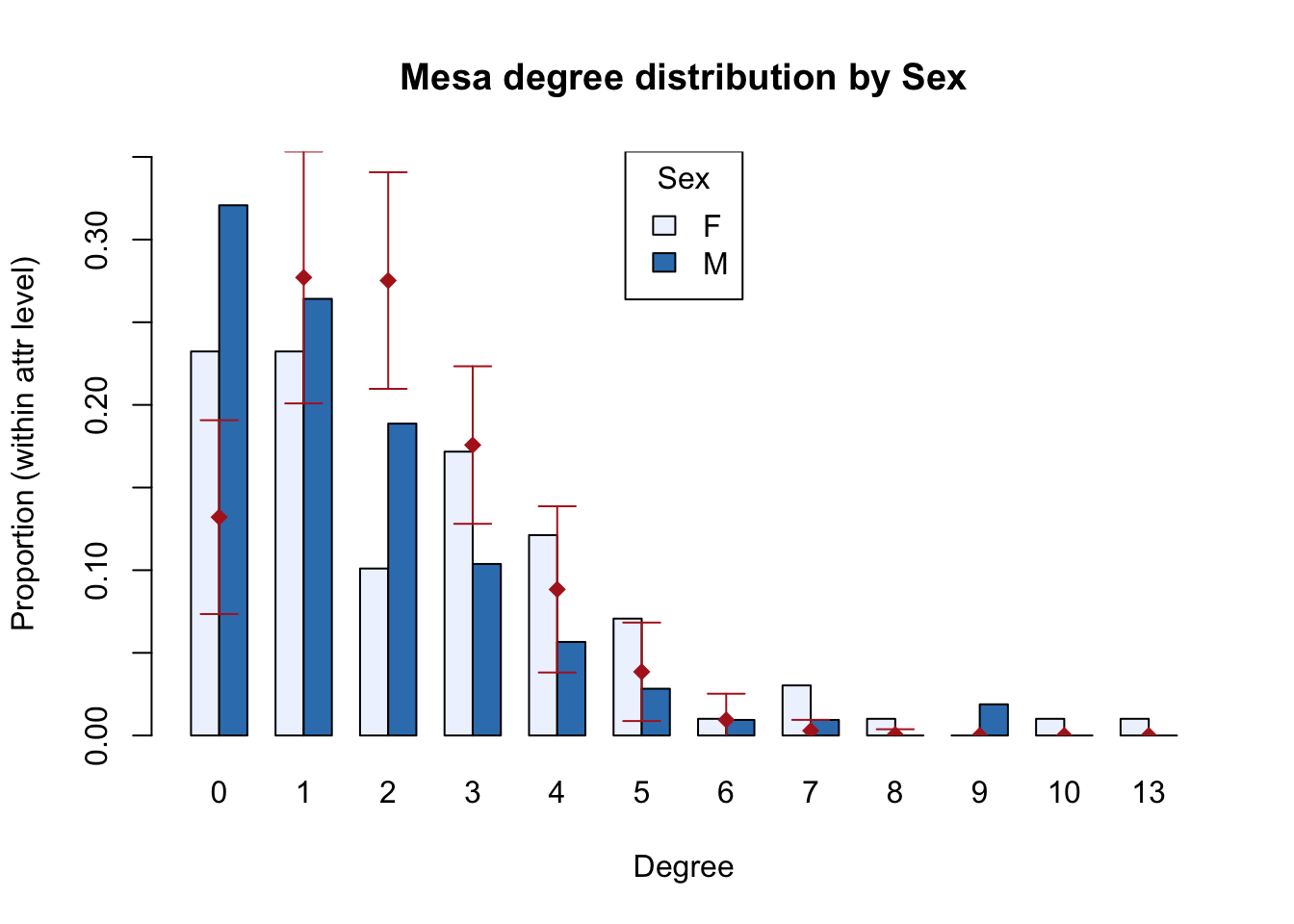
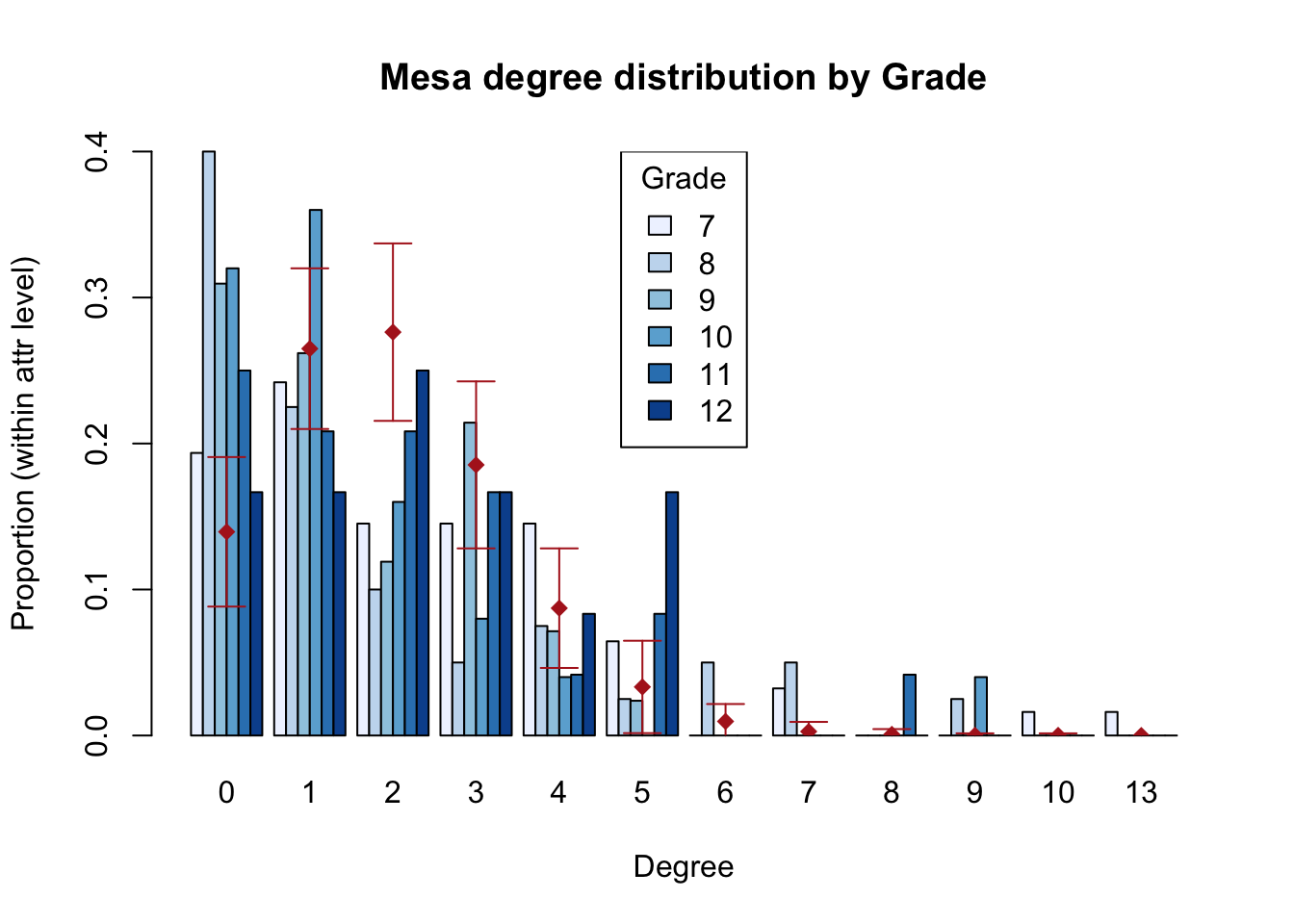
Otherwise, we’ll look at one important thing here: the summary statistics for the model terms from the two types of network data. These stats become the target stats in the fitting process.

Code 
cbind(
  network = summary(mesa ~ edges + 
                      nodefactor("Grade") + nodematch("Grade") +
                      nodefactor("Sex") +   nodematch("Sex") +
                      degree(0, by = "Sex")),
  egocensus = summary(mesa.ego ~ edges + 
                        nodefactor("Grade") + nodematch("Grade") +
                        nodefactor("Sex") + nodematch("Sex") +
                        degree(0, by = "Sex")))
                    network egocensus
edges                   203       203
nodefactor.Grade.8       75        75
nodefactor.Grade.9       65        65
nodefactor.Grade.10      36        36
nodefactor.Grade.11      49        49
nodefactor.Grade.12      28        28
nodematch.Grade         163       163
nodefactor.Sex.M        171       171
nodematch.Sex           132       132
deg0.Sex.F               23        23
deg0.Sex.M               34        34

They’re identical. So, net of stochastic variation in the fitting algorithm, the ERGM and TERGM fits from these two different network data inputs should be the same.

29.2.4 Fit the network model

We fit the TERGM with netest using the same formula we used before. This time, netest will automatically detect that the network object passed on the LHS is an egor object, and it will use ergm.ego for the estimation.

When fit without specific population size controls, the ergm.ego package default assumption is that the true network size is equal to the sample size.

We’ll use this default here, since we took a census of our true population network, Mesa, so our egocentric “sample” actually is the same size as our population network. But we’ll show an example of scaling the fit to a different population network size below.

Code 
set.seed(0)
myfit.ego <- netest(mesa.ego,
                    formation = formation,
                    coef.diss = dissolution_coefs(~offset(edges), 60))

Compare the coefficients from the two fits (the same, net of stochastic variations in the fitting algorithm):

Code 
round(cbind(
  network = myfit$coef.form.crude,
  egocensus = myfit.ego$coef.form.crude,
  diff = myfit$coef.form.crude - myfit.ego$coef.form.crude), 3)
                    network egocensus   diff
edges                -6.123    -6.129  0.006
nodefactor.Grade.8    0.198     0.187  0.010
nodefactor.Grade.9    0.090     0.094 -0.004
nodefactor.Grade.10   0.339     0.337  0.002
nodefactor.Grade.11   0.452     0.454 -0.002
nodefactor.Grade.12   0.779     0.768  0.011
nodematch.Grade       3.005     3.005  0.000
nodefactor.Sex.M     -0.275    -0.275  0.001
nodematch.Sex         0.609     0.619 -0.010
deg0.Sex.F            1.661     1.661  0.000
deg0.Sex.M            1.220     1.216  0.004

Run model diagnostics to check the model goodness of fit with the egodata and plot the results:

Code 
set.seed(0)
mydx.ego <- netdx(myfit, nsims = 25, nsteps = 500, ncores = 5)
plot(mydx.ego)

As with the network census data, the simulations from the egodata census match the target statistics in expectation.

We won’t go on to simulate the epidemic, since the inputs to and syntax for EpiModel from here forward are the same as those used for the Mesa network census above.

Note

Bottom line: The basic netest syntax is similar for all types of network data inputs – target statistics, a network census dataset or egocentrically sampled network data.

Since ERGM/TERGM fits depend only on the model’s sufficient statistics, when the values of these statistics are the same, the estimated coefficients, network simulations and epidemic simulations will be the same (up to stochastic variation), regardless of the type of data that you pass to EpiModel.

29.2.5 Scale the fit to a different network size

Using the netest function to estimate the model for a larger (or smaller) network is straightforward, and useful in two contexts:

  1. Your egocentrically sampled dataset is fairly small.

    Egocentric study designs are used just like a sample survey: to collect data from a tiny fraction of the whole population, and use the sample to estimate models and make statistical inferences to the whole population. Sampling is efficient (when it’s done right!). But if your sampled network is too small, this may compromise the estimation. The basic principle is analagous to the general statistical rule of thumb that you want a minimum cell size (of, say, 5) in order to estimate model terms that depend on those cells. In this context you want a large enough “pseudo-population network” size during the MCMC run to provide sufficient statistics that can support estimation. A simple rule of thumb is a pseudo-population network size of 1,000, but the appropriate size depends on the complexity of the model and whether there are sample weight, as in other statistical contexts.

  2. Simulation experiments (“what-ifs” and counterfactuals)

    Say you want to examine whether and how network size influences infection dynamics. One way to do that is to fit the network model with a range of explicit pseudo-population sizes, simulate epidemics on these differently sized networks, and compare the results.

It is helpful to learn a bit more about how the package ergm.ego works if you want to explore model-based network scaling, but the basic netest syntax itself is very simple – you pass the argument ppopsize to ergm.ego via the argument set.control.ergm.ego in netest. Here we demonstrate estimation with pseudo-population network sizes of 1000 and 2000.

Code 
set.seed(0)
myfit.ego.pp1000 <- netest(mesa.ego,
                           formation = formation,
                           coef.diss = dissolution_coefs(~offset(edges), 60),
                           set.control.ergm.ego = ergm.ego::control.ergm.ego(
                             ppopsize = 1000))

set.seed(0)
myfit.ego.pp2000 <- netest(mesa.ego,
                           formation = formation,
                           coef.diss = dissolution_coefs(~offset(edges), 60),
                           set.control.ergm.ego = ergm.ego::control.ergm.ego(
                             ppopsize = 2000))

The control parameter tells ergm.ego to construct a complete network of size ppopsize with the same (proportional) distribution of nodal attributes, same mean degree and appropriately scaled target statistics as those observed in the egocentric sample (or as close as possible if the ppopsize is not a multiple of the sample size). The MCMC fitting algorithm then uses this scaled pseudo-network during estimation.

If you want to inspect the scaled pseudo-network, it can be found in the fit object component newnetwork. This is technically the network used in the last chain of the MCMC estimation process, so the ties are a stochastic draw from the model distribution, but the target stats and nodeset (with attributes) are the same throughout the fitting process.

Compare the number of nodes in each of the networks, their target stats, and the preservation of mean degree across network size (net of stochasticity):

Code 
# network sizes:

cat("Network sizes: \n\n")
Network sizes:
Code 
data.frame(
  network = network.size(myfit$newnetwork),
  egocensus = network.size(myfit.ego$newnetwork),
  egopp1000 = network.size(myfit.ego.pp1000$newnetwork),
  egopp2000 = network.size(myfit.ego.pp2000$newnetwork))
  network egocensus egopp1000 egopp2000
1     205       205      1025      2050
Code 
# scaling factor for network size:

cat("Network size scaling factor: \n\n")
Network size scaling factor:
Code 
data.frame(
  network = network.size(myfit$newnetwork),
  egocensus = network.size(myfit.ego$newnetwork),
  egopp1000 = network.size(myfit.ego.pp1000$newnetwork),
  egopp2000 = network.size(myfit.ego.pp2000$newnetwork)) / network.size(mesa)
  network egocensus egopp1000 egopp2000
1       1         1         5        10
Code 
# target stats:

cat("Target stats: \n\n")
Target stats:
Code 
data.frame(
   network = myfit$target.stats,
   egocensus = myfit.ego$target.stats,
   egopp1000 = myfit.ego.pp1000$target.stats,
   egopp2000 = myfit.ego.pp2000$target.stats)
                    network egocensus egopp1000 egopp2000
edges                   203       203      1015      2030
nodefactor.Grade.8       75        75       375       750
nodefactor.Grade.9       65        65       325       650
nodefactor.Grade.10      36        36       180       360
nodefactor.Grade.11      49        49       245       490
nodefactor.Grade.12      28        28       140       280
nodematch.Grade         163       163       815      1630
nodefactor.Sex.M        171       171       855      1710
nodematch.Sex           132       132       660      1320
deg0.Sex.F               23        23       115       230
deg0.Sex.M               34        34       170       340
Code 
# scaling factor for target stats:

cat("Target stat scaling: \n\n")
Target stat scaling:
Code 
data.frame(
   network = myfit$target.stats,
   egocensus = myfit.ego$target.stats,
   egopp1000 = myfit.ego.pp1000$target.stats,
   egopp2000 = myfit.ego.pp2000$target.stats) / myfit$target.stats
                    network egocensus egopp1000 egopp2000
edges                     1         1         5        10
nodefactor.Grade.8        1         1         5        10
nodefactor.Grade.9        1         1         5        10
nodefactor.Grade.10       1         1         5        10
nodefactor.Grade.11       1         1         5        10
nodefactor.Grade.12       1         1         5        10
nodematch.Grade           1         1         5        10
nodefactor.Sex.M          1         1         5        10
nodematch.Sex             1         1         5        10
deg0.Sex.F                1         1         5        10
deg0.Sex.M                1         1         5        10
Code 
# mean degree:

cat("Mean degree: \n\n")
Mean degree:
Code 
data.frame(
  network = summary(myfit$newnetwork ~ meandeg),
  egocensus = summary(myfit.ego$newnetwork ~ meandeg),
  egopp1000 = summary(myfit.ego.pp1000$newnetwork ~ meandeg),
  egopp2000 = summary(myfit.ego.pp2000$newnetwork ~ meandeg))
        network egocensus egopp1000 egopp2000
meandeg 2.17561  2.234146  1.976585  2.044878

Compare the estimated network model coefficients:

Code 
round(data.frame(
  network = myfit$coef.form.crude,
  egocensus = myfit.ego$coef.form.crude,
  egopp1000 = myfit.ego.pp1000$coef.form.crude,
  egopp2000 = myfit.ego.pp2000$coef.form.crude,
  pct.diff2000 = (100*(myfit$coef.form.crude - myfit.ego.pp2000$coef.form.crude)/myfit$coef.form.crude)), 3)
                    network egocensus egopp1000 egopp2000 pct.diff2000
edges                -6.123    -6.129    -7.669    -8.356      -36.467
nodefactor.Grade.8    0.198     0.187     0.175     0.173       12.650
nodefactor.Grade.9    0.090     0.094     0.079     0.078       14.057
nodefactor.Grade.10   0.339     0.337     0.305     0.304       10.454
nodefactor.Grade.11   0.452     0.454     0.410     0.407        9.979
nodefactor.Grade.12   0.779     0.768     0.697     0.683       12.264
nodematch.Grade       3.005     3.005     2.898     2.889        3.877
nodefactor.Sex.M     -0.275    -0.275    -0.261    -0.260        5.235
nodematch.Sex         0.609     0.619     0.558     0.547       10.263
deg0.Sex.F            1.661     1.661     1.594     1.584        4.666
deg0.Sex.M            1.220     1.216     1.168     1.156        5.224

The key difference is the value of the “edges” coefficient, reflecting a scaling assumption built in to the ergm-ego package.

29.2.5.1 The scaling assumption: mean degree? or density?

The canonical edges coefficient in an ERGM controls the density of the network: the probability of a tie across all possible dyads. Density is related to mean degree as:

\[ Mean Degree = Density * (N-1) \] We can verify this in the original Mesa network:

Code 
mesa.meandeg <- summary(mesa ~ meandeg)
mesa.dens <- summary(mesa ~ density)
mesa.meandeg/mesa.dens
meandeg 
    204

As we scale up the network size, \(N' = k*N\), where \(k\) is 5 and 10 in our scaleup examples above, the number of dyads grows (as the square of the net size). If we use the fitted ERGM from the original Mesa network to simulate a network that is 5 or 10 times higher, the canonical edges coefficient would preserve the network density, but that would force the mean degree to rise, by a factor of \((k-1)*Density\). Using the Mesa network, for example, the mean degree would rise from the observed value of about 2 to about 8 and 20 respectively for our 1000 and 2000 sized networks.

This “density-dependent” behavior does not seem realistic in the context of most human social networks. Instead, it seems more likely that the number of ties a person has are likely to level out at a certain number, regardless of how much the population size increases (or decreases, as long as network size doesn’t drop below mean degree).

Note

The ergm-ego package has a built-in assumption that preserves the mean degree rather than the density when network size is scaled up using the ppopsize argument.

Mean degree is preserved by the scaling the edges coefficient. The adjustment happens automatically in ergm.ego and is a straightforward difference on the log scale: log(orig net size) - log(new net size).

Note that the same assumption, that mean degree is the scale invariant parameter, is used in the EpiModel package, and is invoked when using open-population models.