21 SIS Epidemic Across a Dynamic Network
EpiModel uses temporal exponential-family random graph models (TERGMs) to estimate and simulate complete networks based on individual-level, dyad-level, and network-level patterns of density, degree, assortativity, and other features influencing edge formation and dissolution. Building and simulating network-based epidemic models in EpiModel is a multi-step process. It begins with estimation of a temporal ERGM and continues with simulation of a dynamic network and epidemic processes on top of that network.
In this tutorial, we work through a model of a Susceptible-Infected-Susceptible (SIS) epidemic. One example of an SIS disease would be a bacterial sexually transmitted infection such as Gonorrhea, in which individuals may acquire infection from sexual contact with an infected partner, and then recover from infection either through natural clearance or through antibiotic treatment.
We will use a simplifying assumption of a closed population, in which there are no entries or exits from the network; this may be justified by the short time span over which the epidemic will be simulated.
Download the R script to follow along with this tutorial here.
21.1 Network Model Estimation
To get started, load the EpiModel library.
The first step in our network model is to specify a network structure, including features like size and nodal attributes. The network_initialize function creates an object of class network. Below we show an example of initializing a network of 500 nodes, with no edges between them at the start. Edges represent sexual partnerships (mutual person-to-person contact), so this is an undirected network.
The sizes of the networks represented in this workshop are smaller than what might be used for a research-level model, mostly for computational efficiency. Larger network sizes over longer time intervals are typically used for research purposes.
21.1.1 Model Parameterization
This example will start simple, with a formula that represents the network density and the level of concurrency (overlapping sexual partnerships) in the population. This is a dyad-dependent ERGM, since the probability of edge formation between any two nodes depends on the existence of edges between those nodes and other nodes. The concurrent term is defined as the number of nodes with at least two partners at any time. Following the notation of the tergm package, we specify this using a right-hand side (RHS) formula. In addition to concurrency, we will use a constraint on the degree distribution. This will cap the degree of any person at 3, with no nodes allowed to have 4 or more ongoing partnerships. This type of constraint could reflect a truncated sampling scheme for partnerships within a survey (e.g., respondents only asked about their 3 most recent partners), or a model assumption about limits of human activity.
Target statistics will be the input mechanism for formation model terms. The edges term will be a function of mean degree, or the average number of ongoing partnerships. With an arbitrarily specified mean degree of 0.7, the corresponding target statistic is 175: \(edges = mean \ degree \times \frac{N}{2}\).
We will also specify that 22% of individuals exhibit concurrency (this is slightly higher than the 16% expected in a Poisson model conditional on that mean degree). The target statistic for the number of individuals with a momentary degree of 4 or more is 0, reflecting our assumed constraint.
The dissolution model is parameterized from a mean partnership duration estimated from cross-sectional egocentric data. Dissolution models differ from formation models in two respects. First, the dissolution models are not estimated in an ERGM but instead passed in as a fixed coefficient conditional on which the formation model is to be estimated. The dissolution model terms are calculated analytically using the dissolution_coefs function, the output of which is passed into the netest model estimation function. Second, whereas formation models may be arbitrarily complex, dissolution models are limited to a set of dyad-independent models; these are listed in the dissolution_coefs function help page. The model we will use is an edges-only model, implying a homogeneous probability of dissolution for all partnerships in the network. The average duration of these partnerships will be specified at 50 time steps, which will be days in our model.
Dissolution Coefficients
=======================
Dissolution Model: ~offset(edges)
Target Statistics: 50
Crude Coefficient: 3.89182
Mortality/Exit Rate: 0
Adjusted Coefficient: 3.89182The output from this function indicates both an adjusted and crude coefficient. In this case, they are equivalent. Upcoming workshop material will showcase when they differ as result of exits from the network.
21.1.2 Model Estimation and Diagnostics
In EpiModel, network model estimation is performed with the netest function, which is a wrapper around the estimation functions in the ergm and tergm packages. The function arguments are as follows:
function (nw, formation, target.stats, coef.diss, constraints,
coef.form = NULL, edapprox = TRUE, set.control.ergm = control.ergm(),
set.control.tergm = control.tergm(), set.control.ergm.ego = NULL,
verbose = FALSE, nested.edapprox = TRUE, ...)
NULLThe four arguments that must be specified with each function call are:
nw: an initialized empty network.formation: a RHS formation formula.target.stats: target statistics for the formation model.coef.diss: output object fromdissolution_coefs, containing the dissolution coefficients.
Other arguments that may be helpful to understand when getting started are:
constraints: this is another way of inputting model constraints (seehelp("ergm")).coef.form: sets the coefficient values of any offset terms in the formation model (those that are not explicitly estimated but fixed).edapprox: selects the dynamic estimation method. IfTRUE, uses the direct method, otherwise the approximation method.- Direct method: uses the functionality of the
tergmpackage to estimate the separable formation and dissolution models for the network. This is often not used because of computational time. - Approximation method: uses
ergmestimation for a cross-sectional network (the prevalence of edges) with an analytic adjustment of the edges coefficient to account for dissolution (i.e., transformation from prevalence to incidence). This approximation method may introduce bias into estimation in certain cases (high density and short durations) but these are typically not a concern for the low density cases in epidemiologically relevant networks.
- Direct method: uses the functionality of the
21.1.2.1 Estimation
Because we have a dyad-dependent model, MCMC will be used to estimate the coefficients of the model given the target statistics.
21.1.2.2 Diagnostics
There are two forms of model diagnostics for a dynamic ERGM fit with netest: static and dynamic diagnostics. When the approximation method has been used, static diagnostics check the fit of the cross-sectional model to target statistics. Dynamic diagnostics check the fit of the model adjusted to account for edge dissolution.
When running a dynamic network simulation, it is good to start with the dynamic diagnostics, and if there are fit problems, work back to the static diagnostics to determine if the problem is due to the cross-sectional fit itself or with the dynamic adjustment (i.e., the approximation method). A proper fitting ERGM using the approximation method does not guarantee well-performing dynamic simulations.
Here we will examine dynamic diagnostics only. These are run with the netdx function, which simulates from the model fit object returned by netest. One must specify the number of simulations from the dynamic model and the number of time steps per simulation. Choice of both simulation parameters depends on the stochasticity in the model, which is a function of network size, model complexity, and other factors. The nwstats.formula contains the network statistics to monitor in the diagnostics: it may contain statistics in the formation model and also others. By default, it is the formation model. Finally, we are keeping the “timed edgelist” with keep.tedgelist.
We have also built in parallelization into the EpiModel simulation functions, so it is also possible to run multiple simulations at the same time using your computer’s multi-core design. You can find the number of cores in your system with:
Then you can run the multi-core simulations by specifying ncores (EpiModel will prevent you from specifying more cores than you have available).
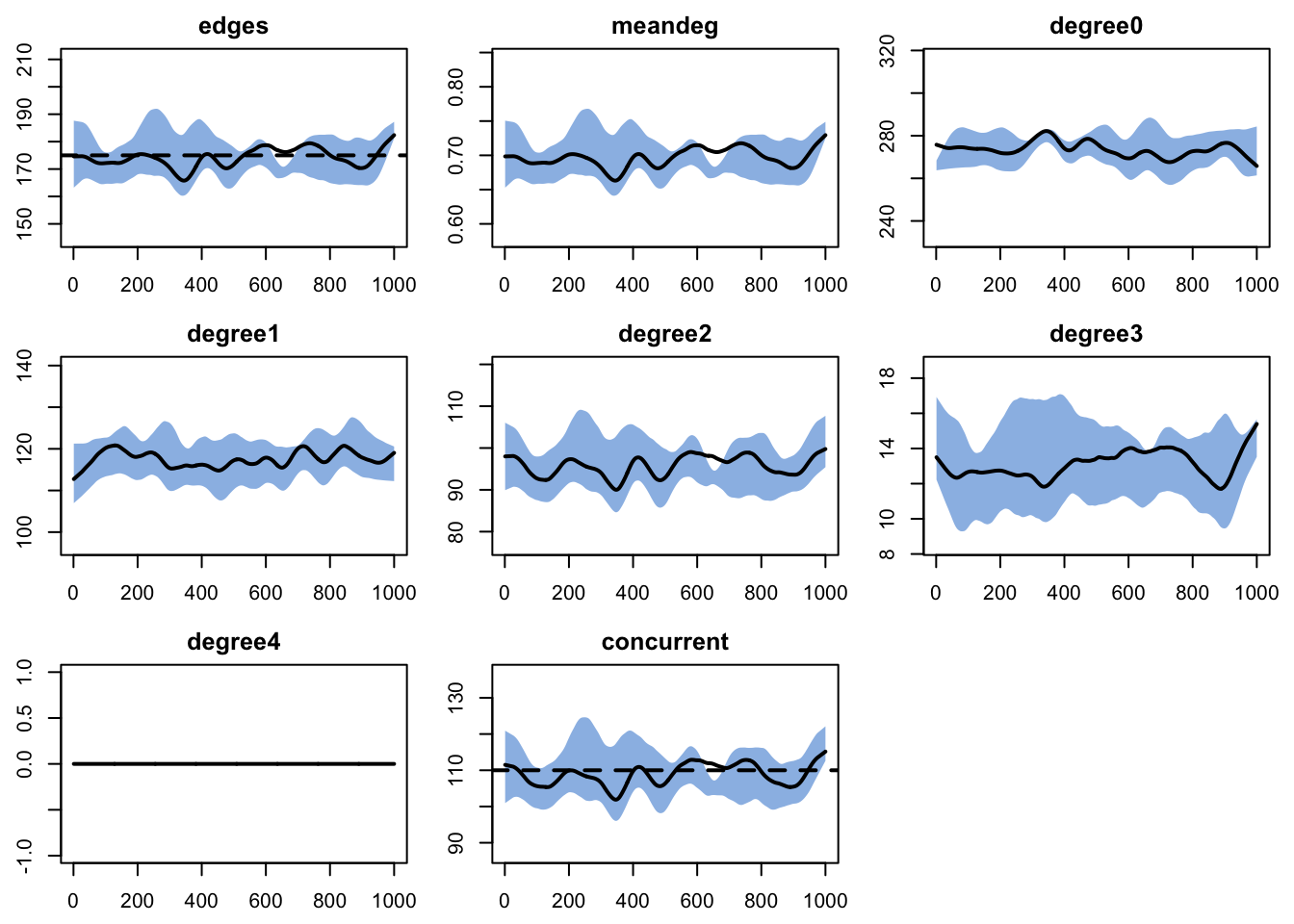
Printing the object will show the object structure and diagnostics. Both formation and duration diagnostics show a good fit relative to their targets. For the formation diagnostics, the mean statistics are the mean of the cross sectional statistics at each time step across all simulations. The Pct Diff column shows the relative difference between the mean and targets. There are two forms of dissolution diagnostics. The edge duration row shows the mean duration of partnerships across the simulations; calculating this involves some imputation due to the length censoring at the start of the simulation. The next row shows the percent of current edges dissolving at each time step; this can be less intuitive than duration, but it does not require the imputation. The percentage of edges dissolution is the inverse of the expected duration: if the duration is 50 days, then we expect that 1/50 (or 2%) to dissolve each day.
EpiModel Network Diagnostics
=======================
Diagnostic Method: Dynamic
Simulations: 10
Time Steps per Sim: 1000
Formation Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
edges 175 174.579 -0.241 1.303 -0.323 5.399 14.137
meandeg NA 0.698 NA 0.005 NA 0.022 0.057
degree0 NA 272.658 NA 1.559 NA 5.810 15.332
degree1 NA 118.742 NA 0.502 NA 2.261 9.747
degree2 NA 95.385 NA 0.698 NA 3.219 11.258
degree3 NA 13.215 NA 0.216 NA 1.136 3.867
degree4 NA 0.000 NA NaN NA 0.000 0.000
concurrent 110 108.600 -1.273 0.856 -1.636 4.149 12.582
Duration Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
edges 50 50.022 0.044 0.311 0.071 1.264 3.661
Dissolution Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
edges 0.02 0.02 0.115 0 0.224 0 0.011Plotting the diagnostics object will show the time series of the target statistics against any targets. The other options used here specify to smooth the mean lines, give them a thicker line width, and plot each statistic in a separate panel. The black dashed lines show the value of the target statistics for any terms in the model. Similar to the numeric summaries, the plots show a good fit over the time series.
The simulated network statistics from diagnostic object may be extracted into a data.frame with get_nwstats.
time sim edges meandeg degree0 degree1 degree2 degree3 degree4 concurrent
1 1 1 186 0.744 257 128 101 14 0 115
2 2 1 187 0.748 255 128 105 12 0 117
3 3 1 192 0.768 254 120 114 12 0 126
4 4 1 190 0.760 257 118 113 12 0 125
5 5 1 188 0.752 257 120 113 10 0 123
6 6 1 184 0.736 256 130 104 10 0 114
7 7 1 188 0.752 257 123 107 13 0 120
8 8 1 189 0.756 256 123 108 13 0 121
9 9 1 191 0.764 254 124 108 14 0 122
10 10 1 188 0.752 254 129 104 13 0 117
11 11 1 188 0.752 255 128 103 14 0 117
12 12 1 192 0.768 248 135 102 15 0 117
13 13 1 193 0.772 248 132 106 14 0 120
14 14 1 192 0.768 248 132 108 12 0 120
15 15 1 191 0.764 248 133 108 11 0 119
16 16 1 189 0.756 248 137 104 11 0 115
17 17 1 186 0.744 250 141 96 13 0 109
18 18 1 189 0.756 250 135 102 13 0 115
19 19 1 193 0.772 249 131 105 15 0 120
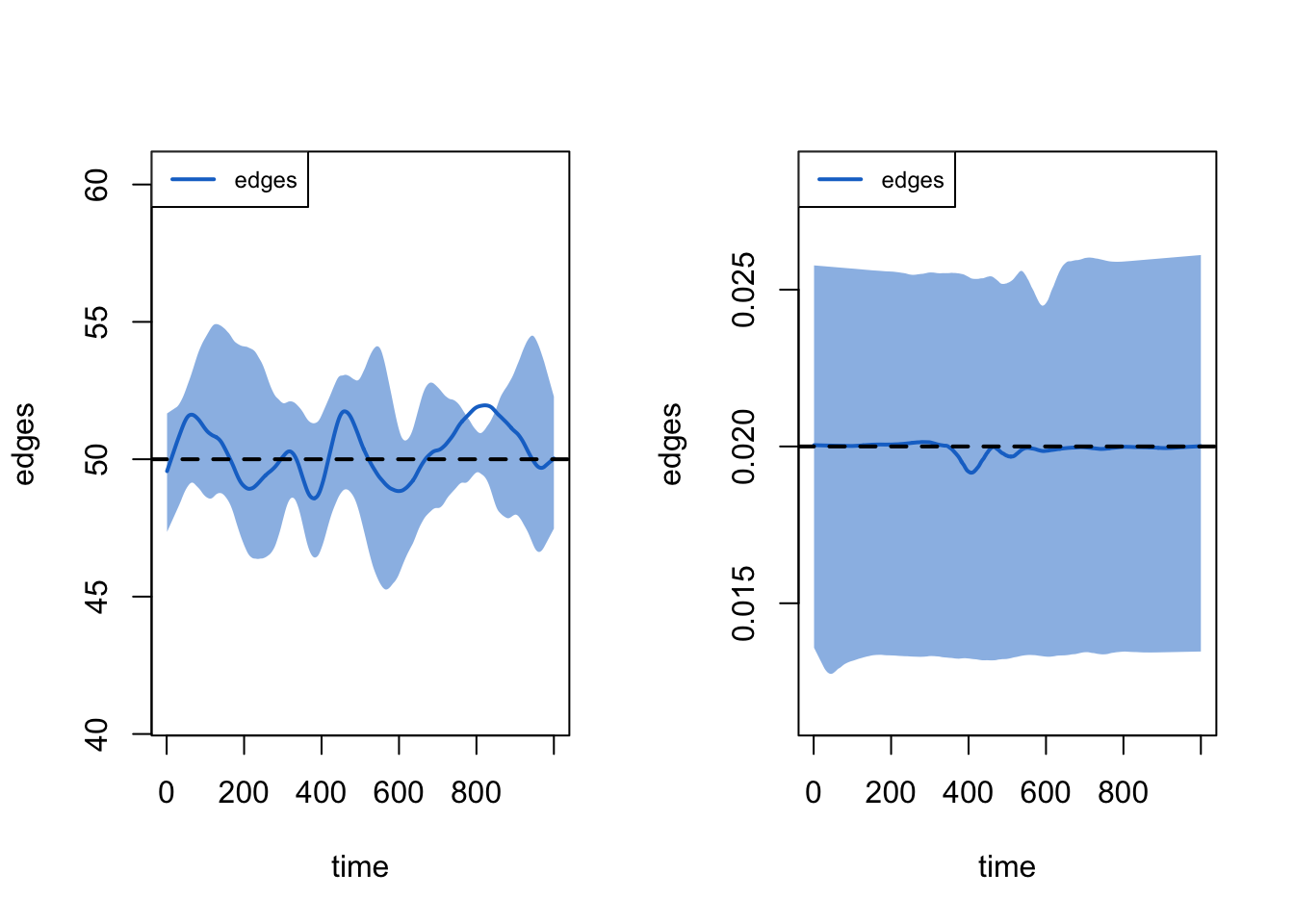
20 20 1 196 0.784 247 129 109 15 0 124The dissolution model fit may also be assessed with plots by specifying either the duration or dissolution type, as defined above. The duration diagnostic is based on the average age of edges at each time step, up to that time step. An imputation algorithm is used for left-censored edges (i.e., those that exist at t1); you can turn off this imputation to see the effects of censoring with duration.imputed = FALSE. Both metrics show a good fit of the dissolution model to the target duration of 50 time steps.
By inspecting the timed edgelist, we can see the burn-in period directly with censoring of onset times. The as.data.frame function is used to extract this edgelist object.
onset terminus tail head onset.censored terminus.censored duration edge.id
1 0 6 1 26 FALSE FALSE 6 1
2 0 29 1 256 FALSE FALSE 29 2
3 0 4 1 419 FALSE FALSE 4 3
4 0 25 2 305 FALSE FALSE 25 4
5 0 80 3 270 FALSE FALSE 80 5
6 0 5 3 281 FALSE FALSE 5 6
7 0 25 3 493 FALSE FALSE 25 7
8 0 27 5 288 FALSE FALSE 27 8
9 0 177 12 185 FALSE FALSE 177 9
10 0 41 13 235 FALSE FALSE 41 10
11 0 10 13 248 FALSE FALSE 10 11
12 0 31 14 43 FALSE FALSE 31 12
13 0 17 14 424 FALSE FALSE 17 13
14 0 111 15 26 FALSE FALSE 111 14
15 0 30 15 277 FALSE FALSE 30 15
16 0 28 17 242 FALSE FALSE 28 16
17 0 40 18 456 FALSE FALSE 40 17
18 0 5 19 94 FALSE FALSE 5 18
19 0 24 23 348 FALSE FALSE 24 19
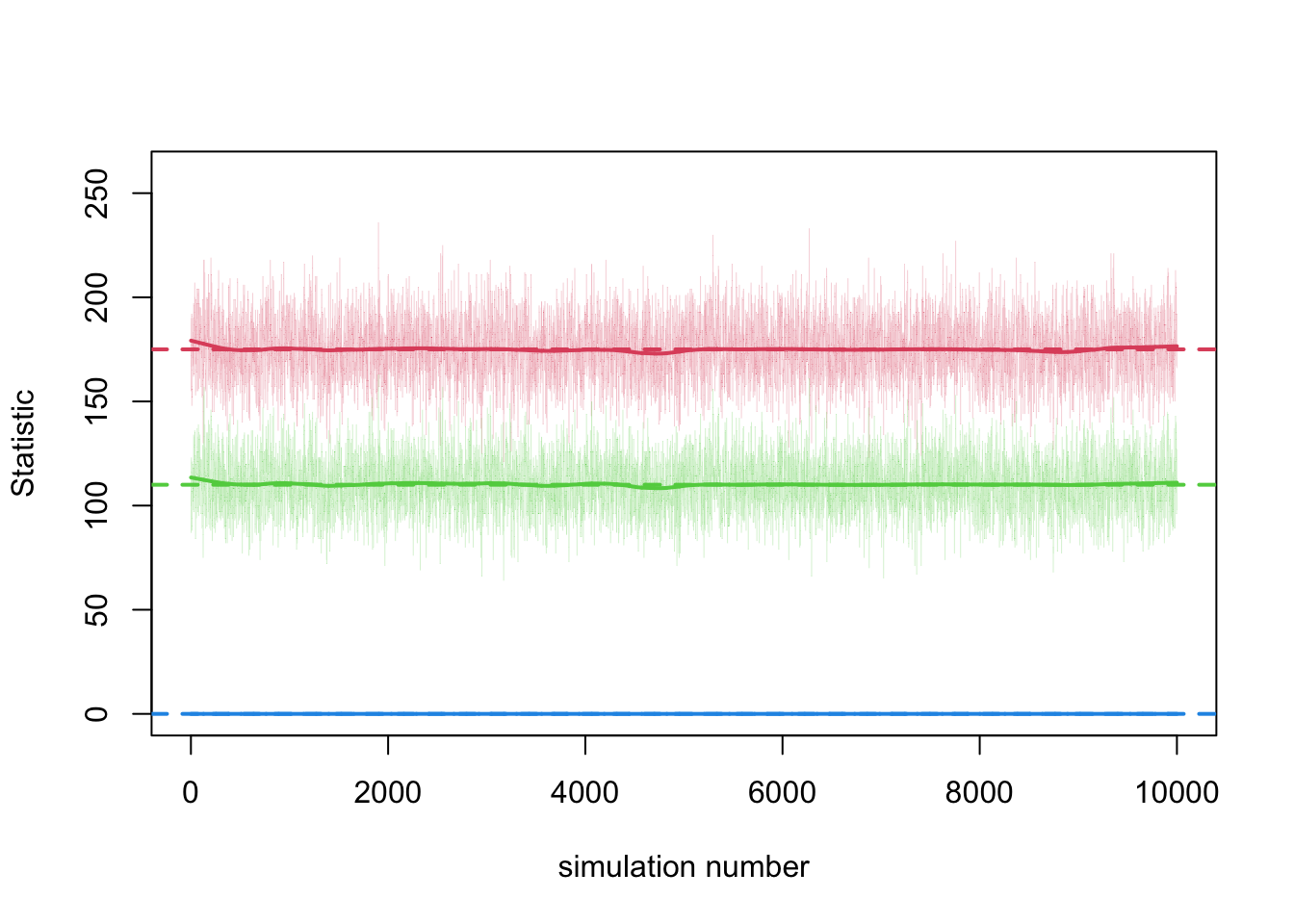
20 0 153 28 88 FALSE FALSE 153 20If the model diagnostics had suggested a poor fit, then additional diagnostics and fitting would be necessary, especially the cross-sectional diagnostics (setting dynamic to FALSE in netdx). Note that the number of simulations may be very large here and there are no time steps specified because each simulation is a cross-sectional network.
The plots now represent individual simulations from an MCMC chain, rather than time steps.
This lack of temporality is now evident when looking at the raw data.
sim edges concurrent deg4+
1 1 190 118 0
2 2 183 121 0
3 3 164 103 0
4 4 170 107 0
5 5 190 118 0
6 6 172 112 0
7 7 183 120 0
8 8 180 111 0
9 9 160 95 0
10 10 170 110 0
11 11 171 104 0
12 12 180 117 0
13 13 163 100 0
14 14 159 104 0
15 15 172 113 0
16 16 184 129 0
17 17 183 114 0
18 18 190 128 0
19 19 195 125 0
20 20 175 109 0If the cross-sectional model fits well but the dynamic model does not, then a full STERGM estimation may be necessary (using edapprox = TRUE). If the cross-sectional model does not fit well, different control parameters for the ERGM estimation may be necessary (see the help file for netdx for instructions).
21.2 Epidemic Simulation
EpiModel simulates disease epidemics over dynamic networks by integrating dynamic model simulations with the simulation of other epidemiological processes such as disease transmission and recovery. Like the network model simulations, these processes are also simulated stochastically so that the range of potential outcomes under the model specifications is estimated.
The specification of epidemiological processes to model may be arbitrarily complex, but EpiModel includes a number of “built-in” model types within the software. Additional components will be programmed and plugged into the simulation API (just like any epidemic model); we will introduce this later, and cover this in depth in our advanced workshop. Here, we will start simple with an SIS epidemic using this built-in functionality. This is just the starting point to what you can do in EpiModel!
21.2.1 Epidemic Model Parameters
Our SIS model will rely on three parameters. The act rate is the number of sexual acts that occur within a partnership each time unit. The overall frequency of acts per person per unit time is a function of the incidence rate of partnerships and this act rate parameter. The infection probability is the risk of transmission given contact with an infected person. The recovery rate for an SIS epidemic is the speed at which infected individuals become susceptible again. For a bacterial STI like gonorrhea, this may be a function of biological attributes like sex or use of therapeutic agents like antibiotics.
EpiModel uses three helper functions to input epidemic parameters, initial conditions, and other control settings for the epidemic model. First, we use the param.net function to input the per-act transmission probability in inf.prob and the number of acts per partnership per unit time in act.rate. The recovery rate implies that the average duration of disease is 10 days (1/rec.rate).
For initial conditions in this model, we only need to specify the number of infected individuals at the outset of the epidemic. The remaining individuals in the network will be classified as disease susceptible.
The control settings specify the structural elements of the model. These include the disease type, number of simulations, and number of time steps per simulation. (Here again we could use the model multi-core functionality by specifying an ncores value, but these models run so quickly that it’s not necessary.)
21.2.2 Simulating the Epidemic Model
Once the model has been parameterized, simulating the model is straightforward. One must pass the fitted network model object from netest along with the parameters, initial conditions, and control settings to the netsim function. With a no-feedback model like this (i.e., there are no vital dynamics parameters), the full dynamic network time series is simulated at the start of each epidemic simulation, and then the epidemiological processes are simulated over that structure.
Printing the model output lists the inputs and outputs of the model. The output includes the sizes of the compartments (s.num is the number susceptible and i.num is the number infected) and flows (si.flow is the number of infections and is.flow is the number of recoveries). Methods for extracting this output is discussed below.
EpiModel Simulation
=======================
Model class: netsim
Simulation Summary
-----------------------
Model type: SIS
No. simulations: 5
No. time steps: 500
No. NW groups: 1
Fixed Parameters
---------------------------
inf.prob = 0.4
act.rate = 2
rec.rate = 0.1
groups = 1
Model Output
-----------------------
Variables: s.num i.num num si.flow is.flow
Networks: sim1 ... sim5
Transmissions: sim1 ... sim5
Formation Statistics
-----------------------
Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
edges 175 172.231 -1.582 2.039 -1.358 5.571 12.989
concurrent 110 106.527 -3.157 1.507 -2.304 3.356 11.877
deg4+ 0 0.000 NaN NaN NaN 0.000 0.000
Duration Statistics
-----------------------
Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
edges 50 49.166 -1.669 0.509 -1.64 0.953 3.308
Dissolution Statistics
-----------------------
Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
edges 0.02 0.02 0.484 0 0.463 0 0.0121.2.3 Model Analysis
Now the the model has been simulated, the next step is to analyze the data. This includes plotting the epidemiological output, the networks over time, and extracting other raw data.
21.2.3.1 Epidemic Plots
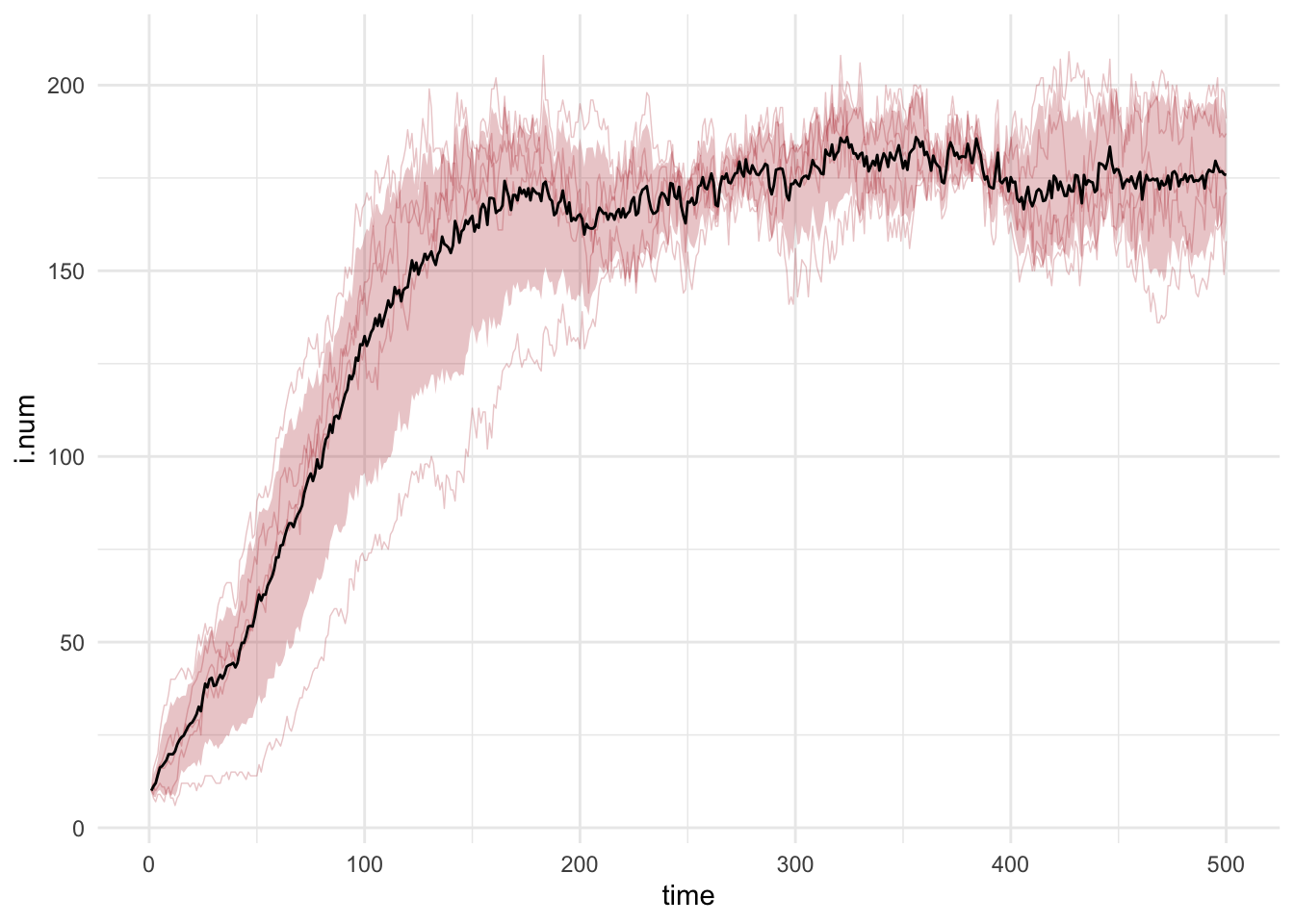
Plotting the output from the epidemic model using the default arguments will display the size of the compartments in the model across simulations. The means across simulations at each time step are plotted with lines, and the polygon band shows the inter-quartile range across simulations.
Graphical elements may be toggled on and off. The popfrac argument specifies whether to use the absolute size of compartments versus proportions.
Code

Whereas the default will print the compartment proportions, other elements of the simulation may be plotted by name with the y argument. Here we plot both flow sizes using smoothed means, which converge at model equilibrium by the end of the time series.
21.2.3.2 Network Plots
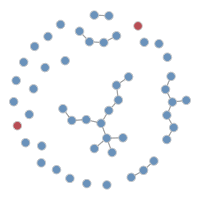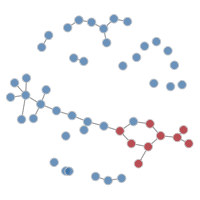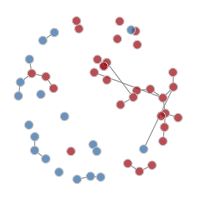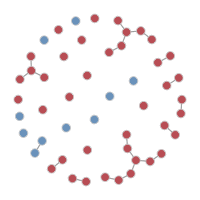
Another available plot type is a network plot to visualize the individual nodes and edges at a specific time point. Network plots are output by setting the type parameter to "network". To plot the disease infection status on the nodes, use the col.status argument: blue indicates susceptible and red infected. It is necessary to specify both a time step and a simulation number to plot these networks.
21.2.3.3 Time-Specific Model Summaries
The summary function with the output of netsim will show the model statistics at a specific time step. Here we output the statistics at the final time step, where roughly two-thirds of the population are infected.
EpiModel Summary
=======================
Model class: netsim
Simulation Details
-----------------------
Model type: SIS
No. simulations: 5
No. time steps: 500
No. NW groups: 1
Model Statistics
------------------------------
Time: 500
------------------------------
mean sd pct
Suscept. 308.6 17.573 0.617
Infect. 191.4 17.573 0.383
Total 500.0 0.000 1.000
S -> I 20.8 4.817 NA
I -> S 19.0 1.225 NA
------------------------------ 21.2.3.4 Data Extraction
The as.data.frame function may be used to extract the model output into a data frame object for easy analysis outside of the built-in EpiModel functions. The function default will output the raw data for all simulations for each time step.
sim time s.num i.num num si.flow is.flow
1 1 1 490 10 500 NA NA
2 1 2 488 12 500 3 1
3 1 3 485 15 500 4 1
4 1 4 483 17 500 3 1
5 1 5 481 19 500 4 2
6 1 6 480 20 500 3 2
7 1 7 476 24 500 4 0
8 1 8 474 26 500 3 1
9 1 9 480 20 500 0 6
10 1 10 476 24 500 5 1 sim time s.num i.num num si.flow is.flow
2491 5 491 311 189 500 20 21
2492 5 492 318 182 500 14 21
2493 5 493 326 174 500 14 22
2494 5 494 321 179 500 26 21
2495 5 495 314 186 500 19 12
2496 5 496 317 183 500 15 18
2497 5 497 319 181 500 19 21
2498 5 498 314 186 500 26 21
2499 5 499 315 185 500 18 19
2500 5 500 314 186 500 21 20Notice that the output above shows all compartment and flow sizes as integers, reinforcing this as an individual-level model.
The out argument may be changed to specify the output of means across the models (with out = "mean").
time s.num i.num num si.flow is.flow
1 1 490.0 10.0 500 NaN NaN
2 2 487.8 12.2 500 3.0 0.8
3 3 486.2 13.8 500 2.8 1.2
4 4 485.4 14.6 500 2.4 1.6
5 5 483.6 16.4 500 3.0 1.2
6 6 482.8 17.2 500 2.4 1.6
7 7 480.8 19.2 500 3.6 1.6
8 8 479.6 20.4 500 2.8 1.6
9 9 482.2 17.8 500 1.0 3.6
10 10 481.2 18.8 500 3.2 2.2 time s.num i.num num si.flow is.flow
491 491 313.8 186.2 500 18.4 21.8
492 492 315.6 184.4 500 18.4 20.2
493 493 318.4 181.6 500 20.8 23.6
494 494 314.2 185.8 500 23.6 19.4
495 495 312.2 187.8 500 19.8 17.8
496 496 314.6 185.4 500 19.6 22.0
497 497 318.4 181.6 500 21.8 25.6
498 498 312.4 187.6 500 26.6 20.6
499 499 310.4 189.6 500 20.2 18.2
500 500 308.6 191.4 500 20.8 19.0The networkDynamic objects are stored in the netsim object, and may be extracted with the get_network function. By default the dynamic networks are saved, and contain the full edge history for every node that has existed in the network, along with the disease status history of those nodes.
NetworkDynamic properties:
distinct change times: 502
maximal time range: 0 until Inf
Dynamic (TEA) attributes:
Vertex TEAs: testatus.active
Includes optional net.obs.period attribute:
Network observation period info:
Number of observation spells: 2
Maximal time range observed: 0 until 501
Temporal mode: discrete
Time unit: step
Suggested time increment: 1
Network attributes:
vertices = 500
directed = FALSE
hyper = FALSE
loops = FALSE
multiple = FALSE
bipartite = FALSE
net.obs.period: (not shown)
vertex.pid = tergm_pid
total edges= 1827
missing edges= 0
non-missing edges= 1827
Vertex attribute names:
active status tergm_pid testatus.active vertex.names
Edge attribute names not shown One thing you can do with that network dynamic object is to extract the timed edgelist of all ties that existed for that simulation.
onset terminus tail head onset.censored terminus.censored duration edge.id
1 0 24 2 13 FALSE FALSE 24 1
2 0 36 2 152 FALSE FALSE 36 2
3 0 109 5 78 FALSE FALSE 109 3
4 0 20 11 173 FALSE FALSE 20 4
5 0 29 13 304 FALSE FALSE 29 5
6 0 27 13 407 FALSE FALSE 27 6
7 0 66 17 168 FALSE FALSE 66 7
8 0 21 22 304 FALSE FALSE 21 8
9 0 46 22 459 FALSE FALSE 46 9
10 0 29 26 164 FALSE FALSE 29 10
11 0 6 26 224 FALSE FALSE 6 11
12 0 1 26 290 FALSE FALSE 1 12
13 0 8 27 112 FALSE FALSE 8 13
14 0 26 27 202 FALSE FALSE 26 14
15 0 34 27 435 FALSE FALSE 34 15
16 0 29 29 63 FALSE FALSE 29 16
17 0 99 29 108 FALSE FALSE 99 17
18 0 41 32 464 FALSE FALSE 41 18
19 0 30 33 75 FALSE FALSE 30 19
20 0 61 34 148 FALSE FALSE 61 20
21 0 58 39 424 FALSE FALSE 58 21
22 0 79 42 113 FALSE FALSE 79 22
23 0 68 42 420 FALSE FALSE 68 23
24 0 104 44 477 FALSE FALSE 104 24
25 0 36 47 487 FALSE FALSE 36 25One can also use the get_transmat function generate a record of some key details about each transmission event that occurred. Shown below are the first 10 transmission events for simulation number 1. The sus column shows the unique ID of the previously susceptible, newly infected node in the event. The inf column shows the ID of the transmitting node. The other columns show the duration of the transmitting node’s infection at the time of transmission, the per-act transmission probability, act rate during the transmission, and final per-partnership transmission rate at that time step (how do we get that?)
# A tibble: 10 × 8
# Groups: at, sus [10]
at sus inf network infDur transProb actRate finalProb
<dbl> <int> <int> <int> <dbl> <dbl> <dbl> <dbl>
1 2 92 173 1 18 0.4 2 0.64
2 2 307 81 1 4 0.4 2 0.64
3 2 416 192 1 2 0.4 2 0.64
4 3 11 173 1 19 0.4 2 0.64
5 3 150 92 1 1 0.4 2 0.64
6 3 223 92 1 1 0.4 2 0.64
7 3 307 81 1 5 0.4 2 0.64
8 4 161 223 1 1 0.4 2 0.64
9 4 297 416 1 2 0.4 2 0.64
10 4 413 307 1 1 0.4 2 0.6421.2.3.5 Data Exporting and Plotting with ggplot
We built in plotting methods directly for netsim class objects so you can easily plot multiple types of summary statistics from the simulated model object. However, if you prefer an external plotting tool in R, such as ggplot, it is easy to extract the data in tidy format for analysis and plotting. Here is an example how to do so for out model above. See the help for the ggplot if you are unfamiliar with this syntax.
Code
df <- as.data.frame(sim)
df.mean <- as.data.frame(sim, out = "mean")
library(ggplot2)
ggplot() +
geom_line(data = df, mapping = aes(time, i.num, group = sim), alpha = 0.25,
lwd = 0.25, color = "firebrick") +
geom_bands(data = df, mapping = aes(time, i.num),
lower = 0.1, upper = 0.9, fill = "firebrick") +
geom_line(data = df.mean, mapping = aes(time, i.num)) +
theme_minimal()