46  Starting a COVID Model

In this tutorial, we will build on our SEIR model for COVID-19 by adding demography (aging, births, and deaths). This will involve learning a few new components of the EpiModel extension API.

Note

This tutorial has two R scripts you should download: a primary script containing the code below and a separate module script. Download both and put them in the same working directory.

46.1 Setup

First start by loading EpiModel and clearing your global environment.

library(EpiModel)
rm(list = ls())

We will use the extension infection and disease progression modules from Day 4. Like the models with extension modules we ran then, we will keep the functions within one R script and the code to run the model in another script. For the purposes of this tutorial, we will show them bundled together but the linked files are split.

We will start with the initialization of the network object, with the relevant age and disease status attributes, then show the new epidemic models, then the network model estimation, and then epidemic model parameterization and simulation. In practice, we would typically go back and forth many times between all of these components.

46.2 Network Initialization

The model will represent age as a continuous nodal attribute. Aging will increment this attribute for everyone by a day (the value of the time step) in a linear fashion, and mortality will be a function of age.

To start, we initialize the range of possible ages (in years) at the outset.

ages <- 0:85

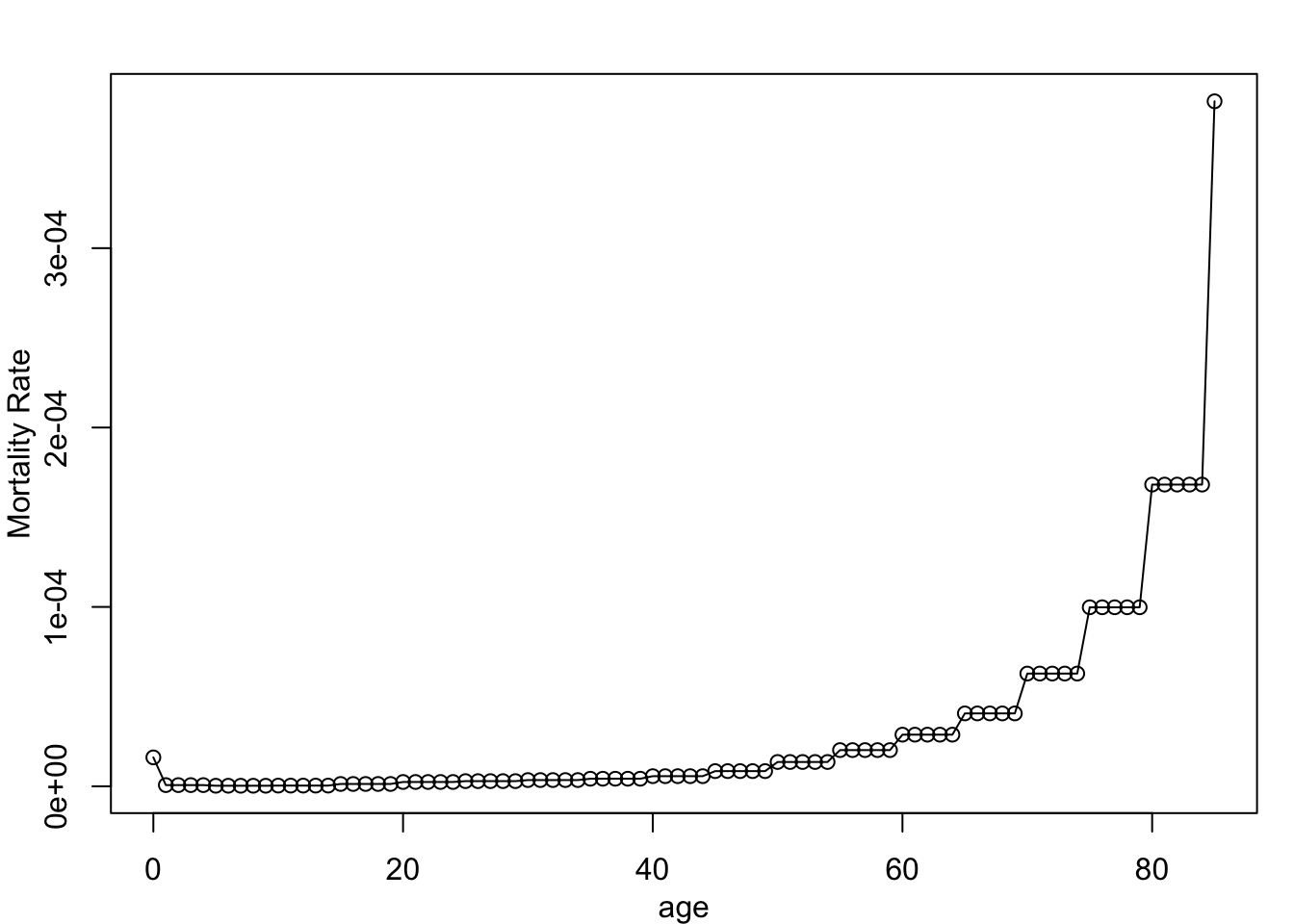
Next, we calculate age-specific mortality rates based on one demographic table online. This lists the rates per year per 100,000 persons in the United States by age groups, in the following age bands:

# Rates per 100,000 for age groups: <1, 1-4, 5-9, 10-14, 15-19, 20-24, 25-29,
#                                   30-34, 35-39, 40-44, 45-49, 50-54, 55-59,
#                                   60-64, 65-69, 70-74, 75-79, 80-84, 85+
departure_rate <- c(588.45, 24.8, 11.7, 14.55, 47.85, 88.2, 105.65, 127.2,
                    154.3, 206.5, 309.3, 495.1, 736.85, 1051.15, 1483.45,
                    2294.15, 3642.95, 6139.4, 13938.3)

To convert this to a per-capita daily death rate, we divide by 365,000:

dr_pp_pd <- departure_rate / 1e5 / 365

Next we build out a vector of daily death rates by repeating the rate above by the size of the age band. Now we have a rate for each age, with some repeats within age band.

age_spans <- c(1, 4, rep(5, 16), 1)
dr_vec <- rep(dr_pp_pd, times = age_spans)
head(data.frame(ages, dr_vec), 20)

   ages       dr_vec
1     0 1.612192e-05
2     1 6.794521e-07
3     2 6.794521e-07
4     3 6.794521e-07
5     4 6.794521e-07
6     5 3.205479e-07
7     6 3.205479e-07
8     7 3.205479e-07
9     8 3.205479e-07
10    9 3.205479e-07
11   10 3.986301e-07
12   11 3.986301e-07
13   12 3.986301e-07
14   13 3.986301e-07
15   14 3.986301e-07
16   15 1.310959e-06
17   16 1.310959e-06
18   17 1.310959e-06
19   18 1.310959e-06
20   19 1.310959e-06

It ends up looking like this visually:

par(mar = c(3,3,2,1), mgp = c(2,1,0), mfrow = c(1,1))
plot(ages, dr_vec, type = "o", xlab = "age", ylab = "Mortality Rate")

We will now add age and disease status attributes to an initialized network object. We will use a larger population size than last time:

n <- 1000
nw <- network_initialize(n)

For each node, we will randomly sample an age from the vector of ages (from 0 to 85), and then set that as a vertex attribute on the network object.

ageVec <- sample(ages, n, replace = TRUE)
nw <- set_vertex_attribute(nw, "age", ageVec)

This model will also initialize people into a latent (E state) disease stage.

statusVec <- rep("s", n)
init.latent <- sample(1:n, 50)
statusVec[init.latent] <- "e"
table(statusVec)

statusVec
  e   s 
 50 950 

which(statusVec == "e")

 [1]  19  26  45  73  77 108 133 153 180 183 205 216 217 338 351 354 373 396 422
[20] 446 460 474 502 528 533 534 546 558 563 566 660 668 680 689 691 696 699 712
[39] 738 746 760 779 833 840 909 915 942 956 961 987

Because of that we will manually set up a vector of disease statuses and set it on the network object as a status attribute. This is an alternative way to set up disease status, instead of using the initial conditions in init.net.

nw <- set_vertex_attribute(nw, "status", statusVec)
nw

 Network attributes:
  vertices = 1000 
  directed = FALSE 
  hyper = FALSE 
  loops = FALSE 
  multiple = FALSE 
  bipartite = FALSE 
  total edges= 0 
    missing edges= 0 
    non-missing edges= 0 

 Vertex attribute names: 
    age status vertex.names 

No edge attributes

46.3 Demographic Modules

With the network initialized, we will now turn to building out the three new extension modules. This set of extensions will add three demographic processes to the model: aging, births, and deaths. The birth and death processes in particular will involve some specific changes to the nodes that must be completed under the EpiModel extension API.

46.3.1 Aging

The aging module performs one simple process: to update the age attribute (in years) of everyone on the network by a day (or 1/365 years). It does this by getting the age attribute from the dat object, updating the vector, and then setting it back on the dat object. The function design follows the same format as our SEIR modules in Day 4.

aging <- function(dat, at) {

  age <- get_attr(dat, "age")
  age <- age + 1/365
  dat <- set_attr(dat, "age", age)

  dat <- set_epi(dat, "meanAge", at, mean(age, na.rm = TRUE))

  return(dat)
}

We also add a new summary statistic, meanAge, which is the mean of the age vector for that time step.

46.3.2 Mortality

For the mortality module, we will implement a process of age-specific mortality with an excess risk of death with active infection. The process is more complex than the built-in departures module (which might cover death but other forms of exit from the population). We will step through the function together in the tutorial.

Note that the overall design of the function is similar to any other EpiModel extension module. The get_ and set_ functions are used to read and write to the dat object. The individual process of mortality involves querying the death rates by the age of active nodes, and then drawing from a binomial distribution for each eligible node.

EpiModel API Rule: For nodes who have died, two specific nodal attributes must be updated: active and exitTime. Upon death, the active value of those nodes turns from 1 to 0. The exitTime is the current time step, at. These two nodal attributes must be updated in a death (or other departure) module to tell EpiModel how to appropriately update the network object at the end of the time step (which you never have to worry about).

dfunc <- function(dat, at) {

  ## Attributes
  active <- get_attr(dat, "active")
  exitTime <- get_attr(dat, "exitTime")
  age <- get_attr(dat, "age")
  status <- get_attr(dat, "status")

  ## Parameters
  dep.rates <- get_param(dat, "departure.rates")
  dep.dis.mult <- get_param(dat, "departure.disease.mult")

  ## Query alive
  idsElig <- which(active == 1)
  nElig <- length(idsElig)

  ## Initialize trackers
  nDepts <- 0
  idsDepts <- NULL

  if (nElig > 0) {

    ## Calculate age-specific departure rates for each eligible node ##
    ## Everyone older than 85 gets the final mortality rate
    whole_ages_of_elig <- pmin(ceiling(age[idsElig]), 86)
    drates_of_elig <- dep.rates[whole_ages_of_elig]

    ## Multiply departure rates for diseased persons
    idsElig.inf <- which(status[idsElig] == "i")
    drates_of_elig[idsElig.inf] <- drates_of_elig[idsElig.inf] * 
                                   dep.dis.mult

    ## Simulate departure process
    vecDepts <- which(rbinom(nElig, 1, drates_of_elig) == 1)
    idsDepts <- idsElig[vecDepts]
    nDepts <- length(idsDepts)

    ## Update nodal attributes
    if (nDepts > 0) {
      active[idsDepts] <- 0
      exitTime[idsDepts] <- at
    }
  }

  ## Set updated attributes
  dat <- set_attr(dat, "active", active)
  dat <- set_attr(dat, "exitTime", exitTime)
  
  ## Summary statistics ##
  dat <- set_epi(dat, "total.deaths", at, nDepts)

  # covid deaths
  covid.deaths <- length(intersect(idsDepts, which(status == "i")))
  dat <- set_epi(dat, "covid.deaths", at, covid.deaths)

  return(dat)
}

Note that the overall process of mortality involves flipping a coin for each eligible person in the population, weighted by their age and disease status, and keeping track of who came up as heads (i.e., a 1). We end the function by saving two summary statistics that count the overall deaths and the COVID-related deaths separately.

46.3.3 Births

Finally, we add a new arrivals module to handle births (there may be other forms of arrivals such as in-migration that we would like to handle separately) but not in this model. In terms of the process, births is a simple function of the current population size times a fixed birth rate. This is stochastic at each time step by drawing an non-negative integer from a Poisson distribution.

EpiModel API Rule: If there are any births, then all the nodal attributes for incoming nodes must be specified. At a minimum, all EpiModel models must have these 5 attributes: active, status, infTime, entrTime, and exitTime. The append_core_attr function automatically handles the updating of the active, entrTime, and exitTime attributes, since these will be uniform across models. Users are responsible for updating status and infTime with the desired incoming values, using the append_attr function. Any other nodal attributes specific to your model, such as age in our current model, should also be appended using this approach. The append_attr function allows you to write those standard values to the end of the attribute vectors, where new nodes are “placed” in terms of their position on the vector. append_attr can either take a single value (repeated for all new arrivals) or a vector of values that may be unique for each arrival.

afunc <- function(dat, at) {

  ## Parameters ##
  n <- get_epi(dat, "num", at - 1)
  a.rate <- get_param(dat, "arrival.rate")

  ## Process ##
  nArrivalsExp <- n * a.rate
  nArrivals <- rpois(1, nArrivalsExp)

  # Update attributes
  if (nArrivals > 0) {
    dat <- append_core_attr(dat, at = at, n.new = nArrivals)
    dat <- append_attr(dat, "status", "s", nArrivals)
    dat <- append_attr(dat, "infTime", NA, nArrivals)
    dat <- append_attr(dat, "age", 0, nArrivals)
  }

  ## Summary statistics ##
  dat <- set_epi(dat, "a.flow", at, nArrivals)

  return(dat)
}

We close the function by adding a summary statistic for the number of births.

46.4 Network Model Estimation

With the new modules defined, we can return to parameterizing the network model. Recall that we have initialized the network and set the age and status attributes on the network above.

nw

 Network attributes:
  vertices = 1000 
  directed = FALSE 
  hyper = FALSE 
  loops = FALSE 
  multiple = FALSE 
  bipartite = FALSE 
  total edges= 0 
    missing edges= 0 
    non-missing edges= 0 

 Vertex attribute names: 
    age status vertex.names 

No edge attributes

Next we will parameterize the model starting with the same terms as our last SEIR model, but adding an absdiff term for age. This will control the average absolute difference in ages between any two nodes. With a small target statistic, this will allow for continuous age homophily (assortative mixing).

formation <- ~edges + degree(0) + absdiff("age")

For target statistics, we will start with mean degree, transform that to the expected edges, and then calculate the number of isolates (a synonym for degree(0)) as a proportion of nodes, and absdiff as a function of edges (the target statistic is the sum of all absolute differences in age across all edges, so this is the mean difference times the number of edges).

mean_degree <- 2
edges <- mean_degree * (n/2)
avg.abs.age.diff <- 2
isolates <- n * 0.08
absdiff <- edges * avg.abs.age.diff

target.stats <- c(edges, isolates, absdiff)
target.stats

[1] 1000   80 2000

The dissolution model will use a standard homogeneous dissolution rate, with a death correction here based on the average death rate across the population and a multiplier to account for higher mortality due to COVID. This is not perfect, but this parameter is quite robust to misspecification because the huge differential in average relational duration versus average lifespan (1/mortality rates); notice the minimal change in coefficient with this adjustment.

coef.diss <- dissolution_coefs(~offset(edges), 20, mean(dr_vec)*2)
coef.diss

Dissolution Coefficients
=======================
Dissolution Model: ~offset(edges)
Target Statistics: 20
Crude Coefficient: 2.944439
Mortality/Exit Rate: 6.31841e-05
Adjusted Coefficient: 2.946969

Next we fit the model. You can ignore any warning messages about fitted probabilities that were 0 or 1. These are standard GLM fitting messages. If there is a problem in the model fit, it will emerge in the diagnostics.

est <- netest(nw, formation, target.stats, coef.diss)

We will run the model diagnostics by monitoring both the terms in the model formula and an extension of the degree terms out to degree of 6. We are using an MCMC control setting here to tweak the simulation algorithm to increase the “burn-in” for the Markov chain; this burn-in control is especially helpful in cases of ERGM formulas with absdiff terms (i.e., those with continuous attributes). Although the fit is not perfect here (we are on the cusp of where we also might want to turn off the edges dissolution approximation with edapprox), it is close enough to move forward for this tutorial.

dx <- netdx(est, nsims = 10, ncores = 5, nsteps = 500,
            nwstats.formula = ~edges + absdiff("age") + degree(0:6),
            set.control.tergm = control.simulate.formula.tergm(MCMC.burnin.min = 20000))

Network Diagnostics
-----------------------
- Simulating 10 networks
- Calculating formation statistics

print(dx)

EpiModel Network Diagnostics
=======================
Diagnostic Method: Dynamic
Simulations: 10
Time Steps per Sim: 500

Formation Diagnostics
----------------------- 
            Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
edges         1000  985.676   -1.432  1.714  -8.356         6.268        26.471
absdiff.age   2000 1967.651   -1.617  5.964  -5.424        22.290        81.867
degree0         80   87.789    9.736  0.413  18.857         0.666         9.725
degree1         NA  323.711       NA  0.798      NA         2.999        16.642
degree2         NA  293.035       NA  0.548      NA         2.161        14.528
degree3         NA  175.726       NA  0.497      NA         1.731        12.312
degree4         NA   79.508       NA  0.360      NA         1.802         9.227
degree5         NA   28.707       NA  0.200      NA         1.009         5.540
degree6         NA    8.660       NA  0.102      NA         0.482         2.972

Duration Diagnostics
----------------------- 
      Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
edges     20   19.955   -0.226  0.047  -0.969         0.121         0.589

Dissolution Diagnostics
----------------------- 
      Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
edges   0.05     0.05   -0.021      0  -0.105             0         0.007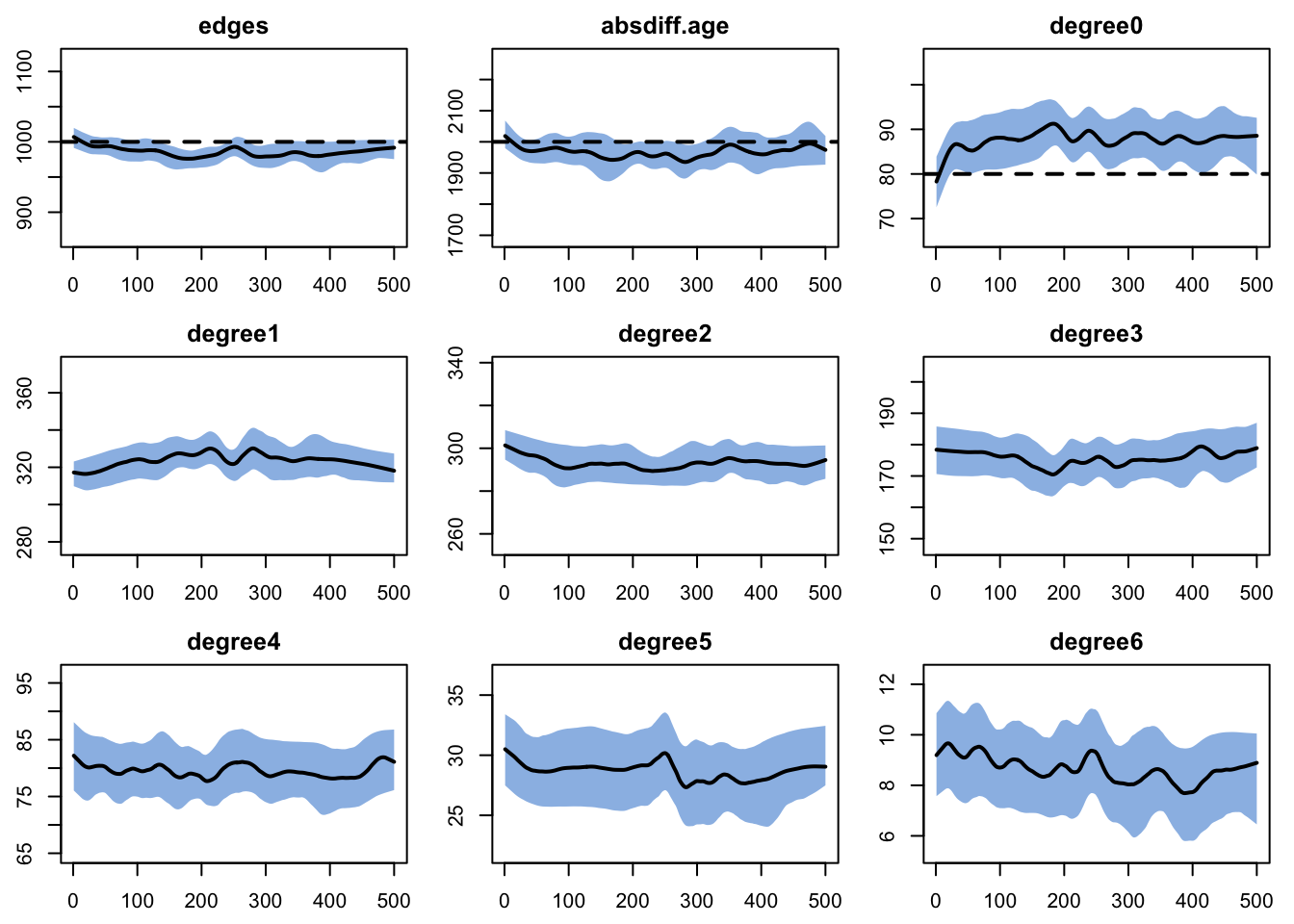

plot(dx)

46.5 EpiModel Model Simulation

To parameterize the model, we need to add the newly referenced model parameters to param.net. These include the departure and arrival rates. Although our past parameters have been scalars (single values), there is nothing to prevent us from passing vectors (or even more structured objects like lists or data frames) as parameters. That is what we do with departure.rates. The departure.disease.mult is the multiplier on the base death rate for persons with active infection (persons in the “i” status). We will assume the arrival rate reflects the average lifespan in days.

param <- param.net(inf.prob = 0.1,
                   act.rate = 3,
                   departure.rates = dr_vec,
                   departure.disease.mult = 100,
                   arrival.rate = 1/(365*85),
                   ei.rate = 0.05, ir.rate = 0.05)

For initial conditions, we have passed in the number initially in the latent state at the outset, so init.net just needs to be a placeholder input.

init <- init.net()

Finally, for control settings, we first source in the new function script (this should now contain five extension functions), and include module names and associated functions for each of the five. Note that these five modules will run in addition to the standard modules that handle initialization, network resimulation, and so on. For this model, we definitely want to resimulate the network at each time step, and we will use tergmLite for computational efficiency. We again use a burn-in control setting for TERGM simulations here, plus add some additional network statistics to monitor for diagnostics.

source("mod15-COVID1-fx.R")
control <- control.net(type = NULL,
                       nsims = 5,
                       ncores = 5,
                       nsteps = 300,
                       infection.FUN = infect,
                       progress.FUN = progress,
                       aging.FUN = aging,
                       departures.FUN = dfunc,
                       arrivals.FUN = afunc,
                       resimulate.network = TRUE,
                       tergmLite = TRUE,
                       set.control.tergm = control.simulate.formula.tergm(MCMC.burnin.min = 10000),
                       nwstats.formula = ~edges + meandeg + degree(0:2) + absdiff("age"))

With all that complete, we now are ready to run netsim. This should take a minute.

sim <- netsim(est, param, init, control)

46.6 Post-Simulation Diagnostics

We run the network diagnostics with the netsim simulations complete to evaluate the potential impact of the epidemic processes on the network diagnostics. Here we see that the three targeted statistics are not maintained at their target levels. Part of this may be due to the general bias in the fit introduced by the edges dissolution approximation, highlighted in the netdx diagnostics above. But the change to the edges and absdiff statistics may be concerning.

plot(sim, type = "formation",
     stats = c("edges", "absdiff.age", "degree0"), plots.joined = FALSE)

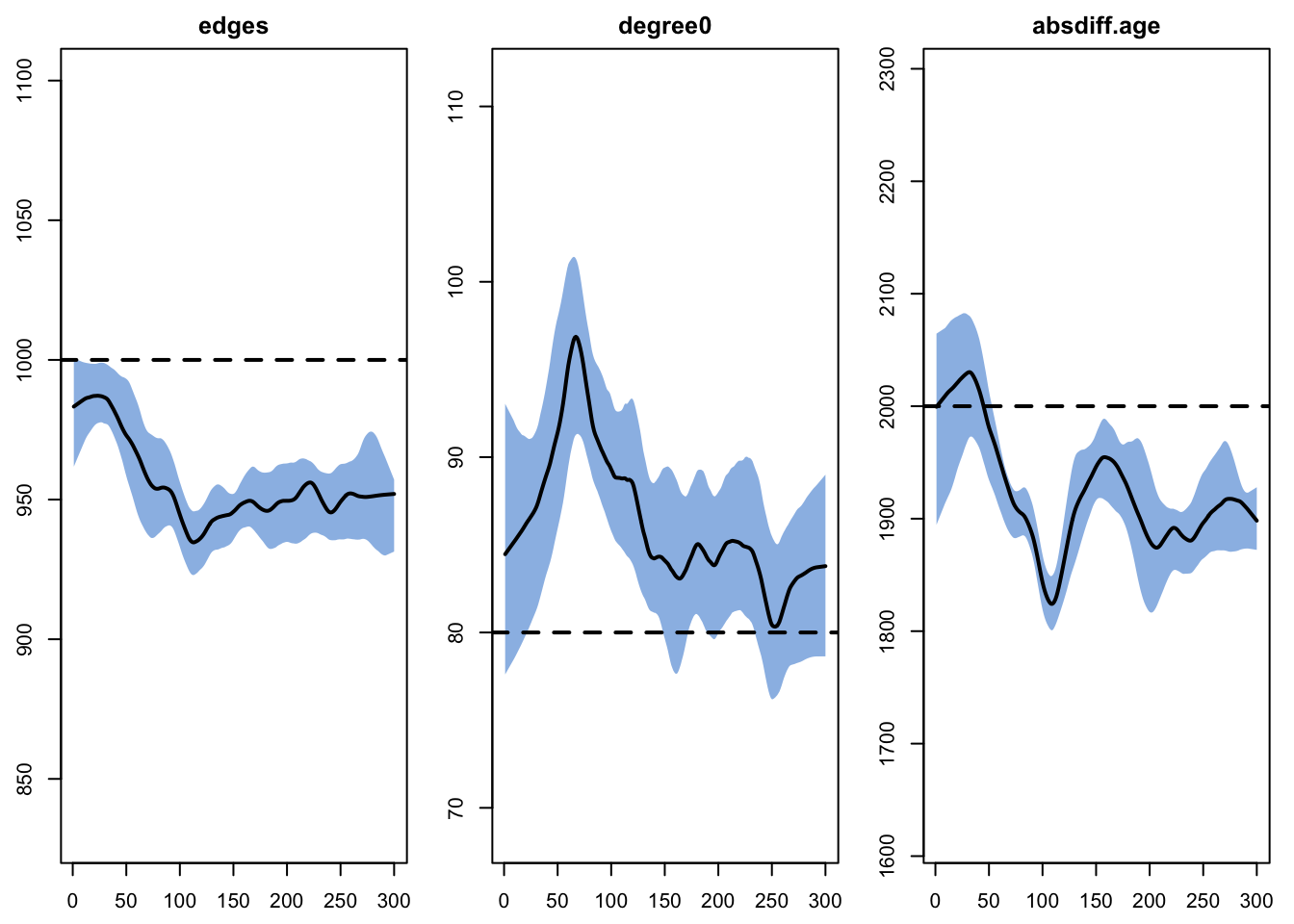
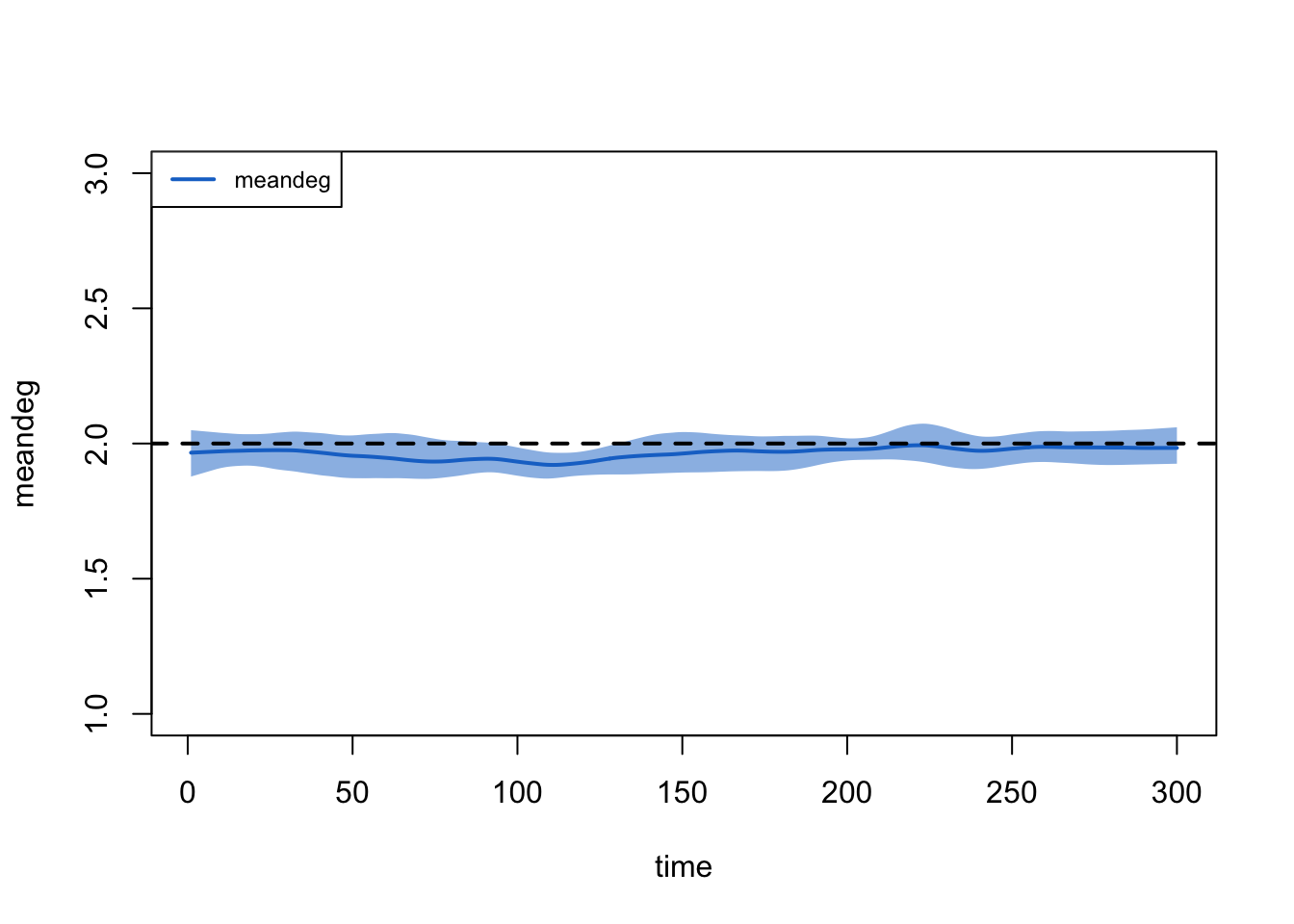
However, it is important to note that the change in edges may be related to underlying reductions in the population size (as a function of relatively high COVID-related mortality). To demonstrate this, we examine the meandeg statistics, which is the per capita mean degree (i.e., it does not depend on the fluctuations in population size). Here, the target statistic is relatively stable (perhaps a minor bias but nothing that will influence the epi outcomes too much).

plot(sim, type = "formation", stats = "meandeg", qnts = 1, ylim = c(1, 3))
abline(h = 2, lty = 2, lwd = 2)

46.7 Epidemic Model Analysis

With the epidemic model simulation complete, let’s inspect the network object. We can see a listing of the modules used, and the model output variables available for inspection. Because we used tergmLite, we only have the summary statistic data and not the individual-level network data.

sim

EpiModel Simulation
=======================
Model class: netsim

Simulation Summary
-----------------------
Model type:
No. simulations: 5
No. time steps: 300
No. NW groups: 1

Fixed Parameters
---------------------------
inf.prob = 0.1
act.rate = 3
departure.rates = 1.612192e-05 6.794521e-07 6.794521e-07 6.794521e-07 
6.794521e-07 3.205479e-07 3.205479e-07 3.205479e-07 3.205479e-07 3.205479e-07 
...
departure.disease.mult = 100
arrival.rate = 3.223207e-05
ei.rate = 0.05
ir.rate = 0.05
groups = 1

Model Functions
-----------------------
initialize.FUN 
resim_nets.FUN 
summary_nets.FUN 
infection.FUN 
departures.FUN 
arrivals.FUN 
nwupdate.FUN 
prevalence.FUN 
verbose.FUN 
progress.FUN 
aging.FUN 

Model Output
-----------------------
Variables: s.num i.num num ei.flow ir.flow e.num r.num 
meanAge se.flow total.deaths covid.deaths a.flow
Networks: sim1 ... sim5
Transmissions: sim1 ... sim5

Formation Statistics
----------------------- 
            Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
edges         1000  955.402   -4.460  3.863 -11.545        10.937        29.154
meandeg         NA    1.965       NA  0.006      NA         0.014         0.053
degree0         80   86.324    7.905  0.781   8.100         1.638         9.812
degree1         NA  316.355       NA  1.496      NA         4.501        17.055
degree2         NA  284.419       NA  0.852      NA         1.743        15.090
absdiff.age   2000 1922.557   -3.872 12.959  -5.976        39.345        91.458


Duration and Dissolution Statistics
----------------------- 
Not available when:
- `control$tergmLite == TRUE`
- `control$save.network == FALSE`
- `control$save.diss.stats == FALSE`
- dissolution formula is not `~ offset(edges)`
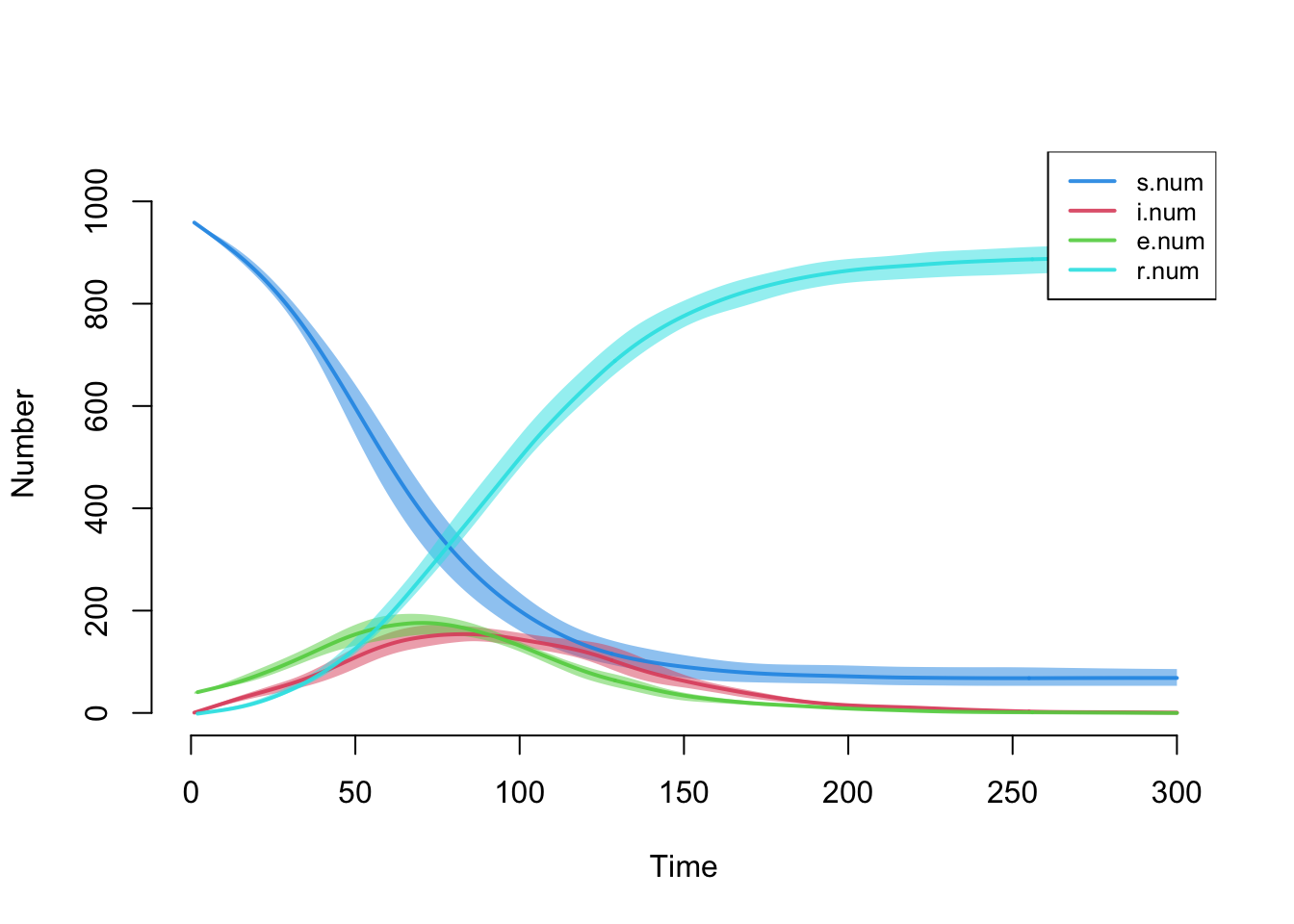
- `keep.diss.stats == FALSE` (if merging)

Here is a default plot of all the compartment sizes (all variables ending in .num), with the full quantile range set to 1.

plot(sim, qnts = 1)

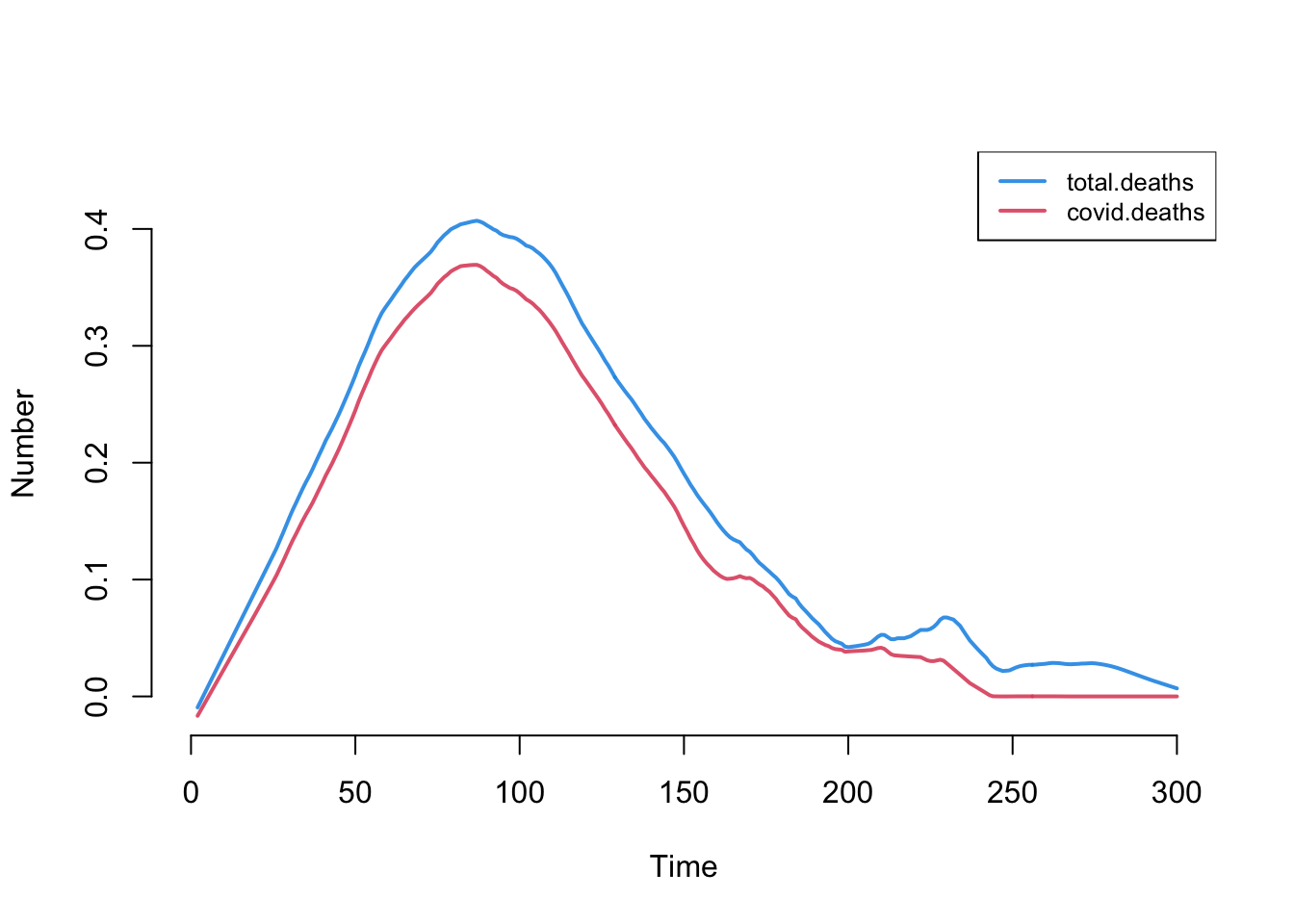
Here is the disease incidence, plotted in two ways:

par(mfrow = c(1,2))
plot(sim, y = "se.flow")
plot(sim, y = "se.flow", mean.smooth = FALSE, qnts = FALSE)

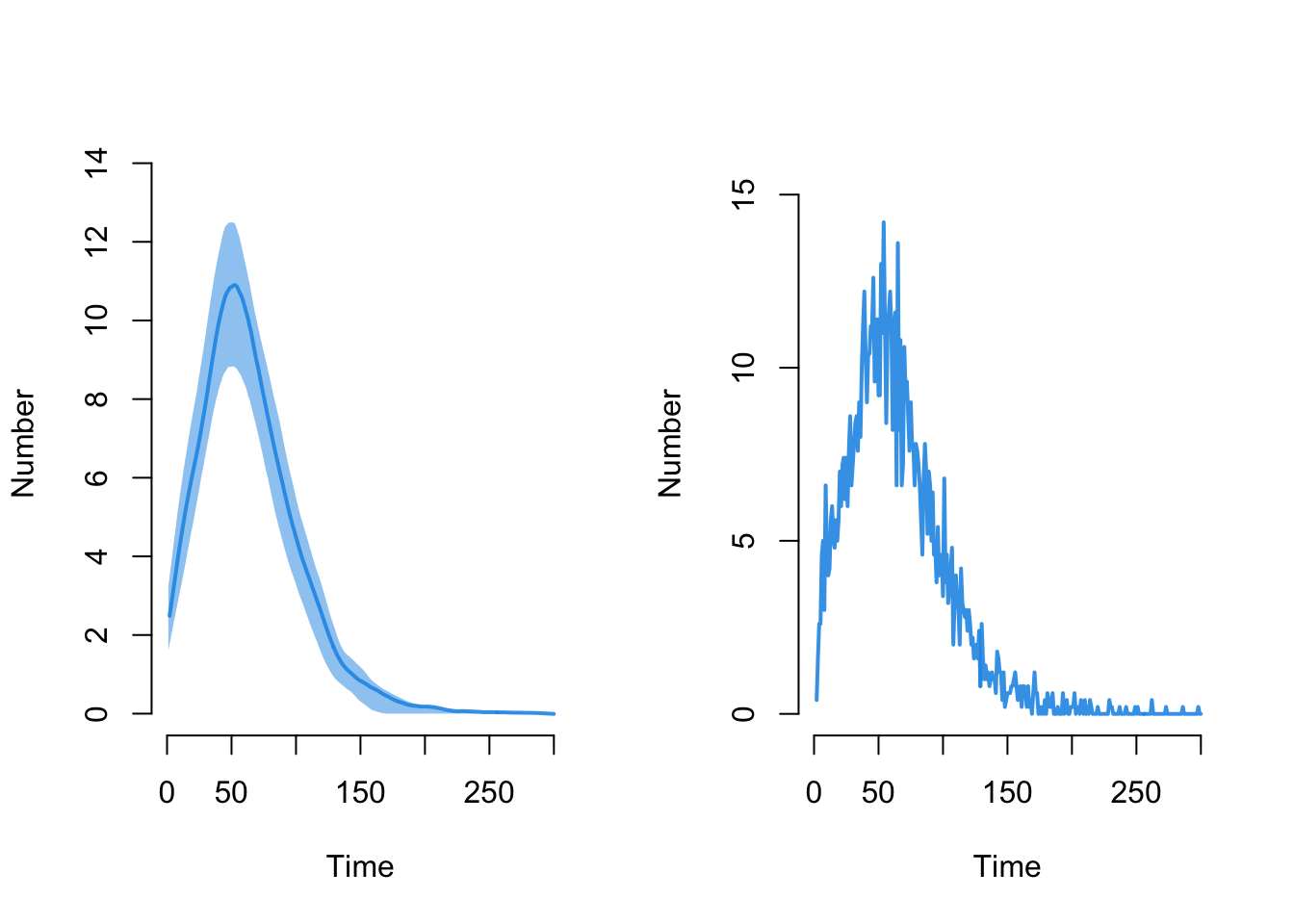
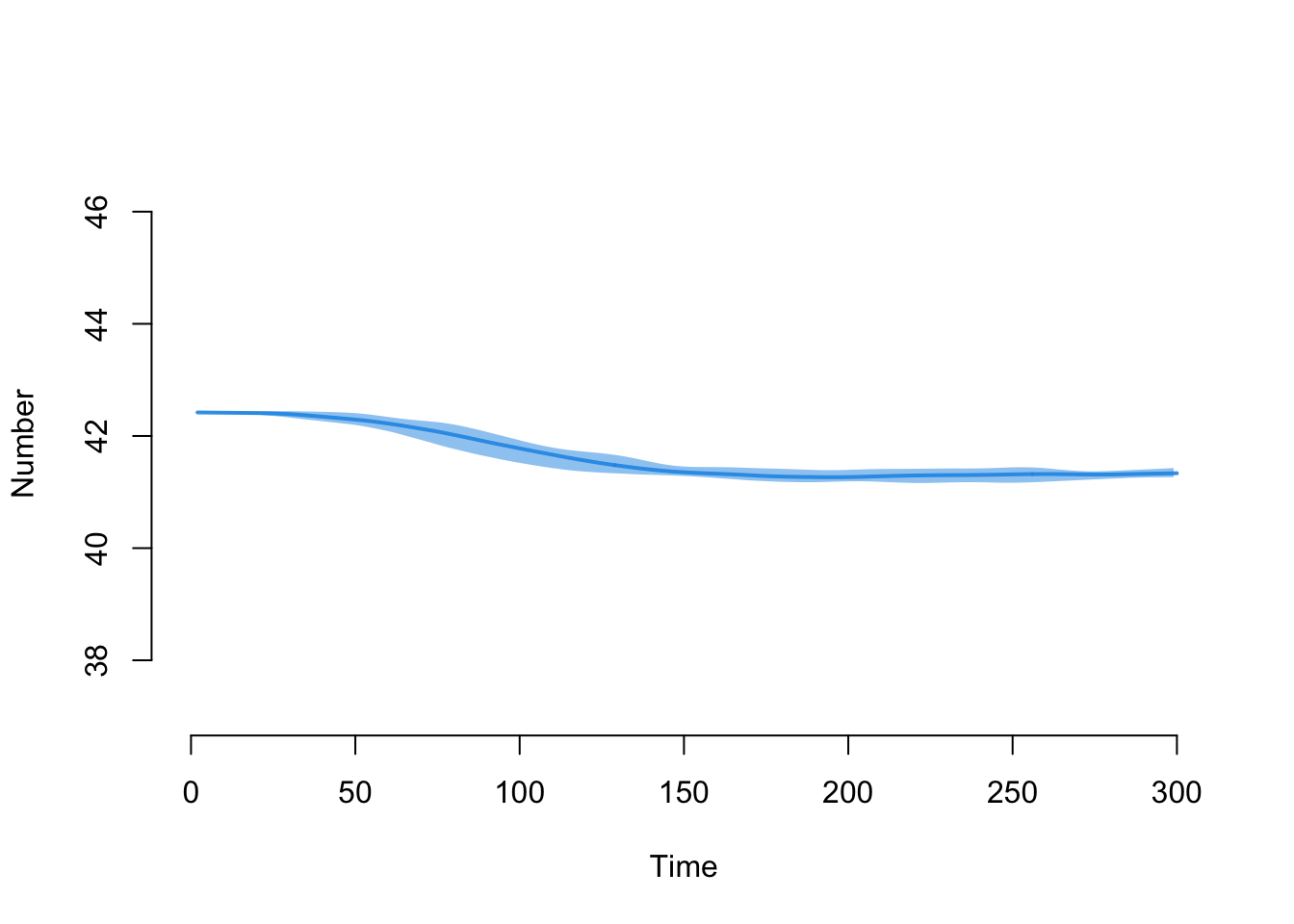
Here is the new mean age summary statistic.

par(mfrow = c(1,1))
plot(sim, y = "meanAge")

Let’s export the data into a data frame that averaged across the simulations and look at the starting and ending numerical values for mean age:

df <- as.data.frame(sim, out = "mean")
head(df$meanAge)

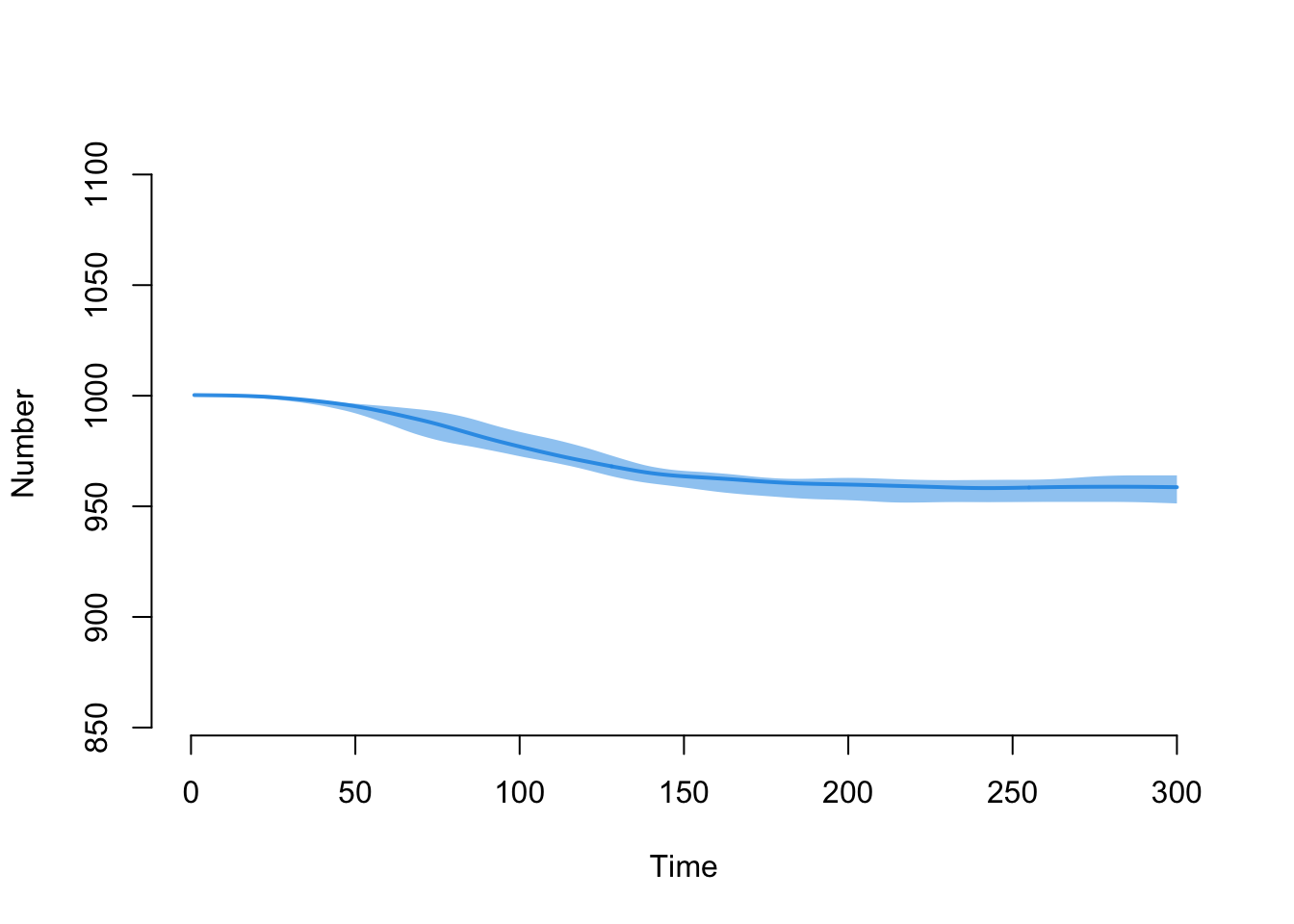
[1]      NaN 42.41974 42.41400 42.41674 42.41948 42.42222

tail(df$meanAge)

[1] 41.33305 41.33579 41.33853 41.33254 41.32604 41.32878

Here is the decline in the overall population size over time:

plot(sim, y = "num")

This plot shows the number of new total and COVID-related deaths each day.

plot(sim, y = c("total.deaths", "covid.deaths"), qnts = FALSE, legend = TRUE)

To demonstrate the transmission tree output for this extension model, we can extract the transmission matrix and then plot a phylogram:

tm1 <- get_transmat(sim)
head(tm1, 20)

# A tibble: 20 × 6
# Groups:   at, sus [20]
      at   sus   inf transProb actRate finalProb
   <dbl> <int> <int>     <dbl>   <dbl>     <dbl>
 1     2    34   915       0.1       3     0.271
 2     2   561   108       0.1       3     0.271
 3     3   408   840       0.1       3     0.271
 4     4    56   840       0.1       3     0.271
 5     4   812   712       0.1       3     0.271
 6     4   865   133       0.1       3     0.271
 7     5   127    77       0.1       3     0.271
 8     6    89   712       0.1       3     0.271
 9     7    81   133       0.1       3     0.271
10     7   253    77       0.1       3     0.271
11     7   906   712       0.1       3     0.271
12     8    37   942       0.1       3     0.271
13     8   212    73       0.1       3     0.271
14     9   141   942       0.1       3     0.271
15     9   270    26       0.1       3     0.271
16     9   666   942       0.1       3     0.271
17     9   888   942       0.1       3     0.271
18    10   360   354       0.1       3     0.271
19    10   395   906       0.1       3     0.271
20    11   113   558       0.1       3     0.271

# Plot the phylogram for the first seed
phylo.tm1 <- as.phylo.transmat(tm1)

found multiple trees, returning a list of 41phylo objects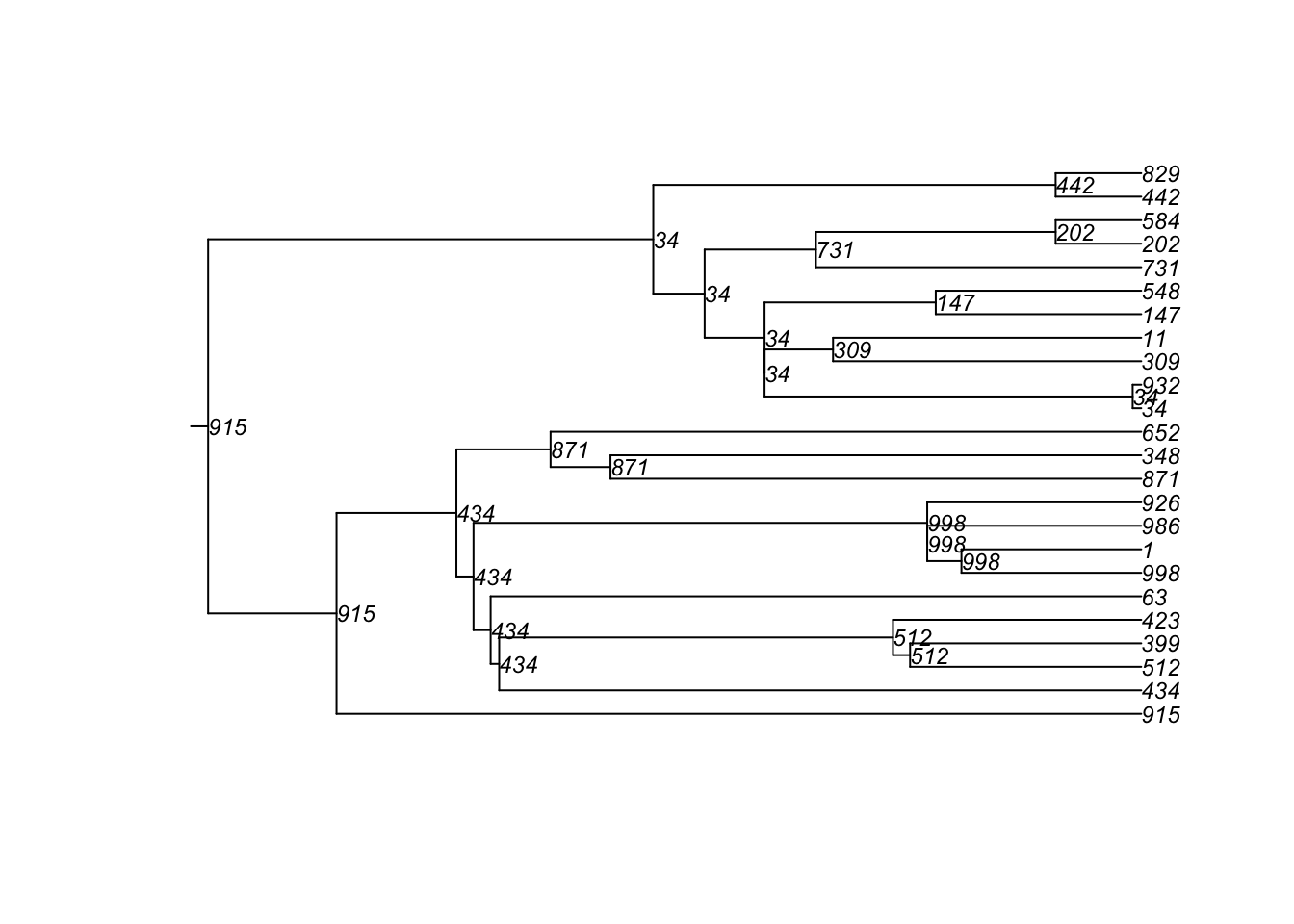

plot(phylo.tm1[[1]], show.node.label = TRUE, root.edge = TRUE, cex = 0.75)

Overall, it appears that our new demographic features of the model are performing well!