| sex | community | num.partners | p1.community | p2.community |
|---|---|---|---|---|
| F | 2 | 0 | NA | NA |
| M | 1 | 0 | NA | NA |
| F | 2 | 0 | NA | NA |
| M | 2 | 0 | NA | NA |
| F | 1 | 2 | 1 | 1 |
| M | 2 | 0 | NA | NA |
| M | 2 | 1 | 2 | NA |
| F | 2 | 1 | 1 | NA |
| F | 2 | 1 | 2 | NA |
| F | 2 | 1 | 2 | NA |
| F | 1 | 0 | NA | NA |
| M | 1 | 2 | 2 | 2 |
| F | 1 | 1 | 1 | NA |
| F | 1 | 1 | 1 | NA |
| M | 2 | 2 | 2 | 1 |
| F | 2 | 1 | 1 | NA |
| M | 1 | 1 | 2 | NA |
| M | 1 | 2 | 1 | 1 |
| M | 2 | 0 | NA | NA |
| M | 2 | 1 | 2 | NA |
41 Lab
This lab provides additional practice with balance and degrees of freedom in the process of specifying and parameterizing a network model.
In real life you would never try to estimate a model with such a small data set! There’s just far too little data. This is for quick pedagogical purposes only.
Also note that everything we are doing here could be automated through the use of the ergm.ego package. This is here to help ensure you understand how the logic works, both so that you can explain it when needed, and so you can do it manually if you ever want or need to.
41.1 Lab questions
41.1.1 Develop and fit network model
The scenario:
- You have a sample of 20 heterosexuals
- They live in two communities
- You want to simulate an artificial population of size 2,000
- You want to include in your model mixing by community as well as sex-specific degree distributions
- You notice that nobody has more than two ongoing ties
- Mean relational age is 187 time steps
- You have extracted their partnerships on the day of the interview, as follows:
We’ve made it relatively easy for you; the sample has the same number of males and females, and the same community breakdown for each. You’re welcome!
Now, you should:
- decide on the network composition of your modeled population
- generate an empty network with those attributes
- determine the model terms you want to include
- calculate target stats for those terms
- put it all together
Note that there are multiple decisions you need to make that don’t have a single correct answer; any choice requires making one or another assumption. At each step, think through what you believe your choice implies.
41.1.2 Simulate epidemic
Then simulate an SIS epidemic with the following features:
- The average act rate per time step is 1.8
- The transmission probability per act is 0.6
- The recovery rate is 0.1
- There are 100 infected females and 100 infected males at the start of the simulation
41.2 Answers
Below is our solution. Don’t take a look until you’ve done it yourself!
41.2.1 Model Initialization
First, we load the EpiModel package.
Next, we initialize a network of 2000 persons in the population.
We then add an attribute for attribute (1000 females, 1000 males). Note we call it group for the reasons mentioned in Module 5; it is a “special” attribute in EpiModel that makes certain functionality easier.
Next, we add a community attribute (800 cmty = 1; 1200 cmty = 2; split evenly across sex).
Use the table function to confirm that the attribute combinations are as expected:
41.2.2 Specify the network model and calculate target stat(s):
We are going to do this iteratively, i.e. decide on one term at a time and calculate its target stat(s):
Overall edges:
Our term here is ~edges. For the target statistic, we have to reconcile the following:
- In our observed data, females and males do not have the same mean degree; females have 0.8 and males have 0.9
- In our model population, the total edges that Fs have with Ms must equal the total edges that Ms have with Fs.
- The size of the two groups is equal in both our sample and our simulated population
- All ties are cross-sex
As we learned the other day, #4 implies that the total ties for males must equal the total ties for females. Adding in #3 implies that in this case mean degree must be equal for females and males.
If we calculated the number of edges as a basis of the male reports, we would get:
And if we did it for females, we would get:
[1] 800Those numbers are not equal. That said, they are not that far off, and perhaps the difference may have been generated by sampling variation given how small the sample is.
Regardless, we have a few options for what we do. Options include:
- Assuming the female reports are accurate and the male are off for some reason (what might be a reason?)
- Assuming the male reports are accurate and the female are off for some reason (what might be a reason?)
- Assuming both are equally accurate and the real value lies in the middle
- Change our assumption about the sex ratio
We’ll go with #3, yielding:
Cross-sex constraint
Next we add the term and associated statistic to limit our model to cross-sex ties. We’ve seen this before; it’s simply the term ~nodematch("group") with target statistic of 0.
Degree 2 constraint
Our data had nobody with degree higher than 2. We can retain this in our model and simulations by using the term (degrange(from = 3)) and setting the target stat to 0.
Note that we could allow for the occasional possibility of a degree above 2 by assigning some positive but very small target statistic. Perhaps it is possible, but just not seen in this small data set. Another reason why you want to have a much larger data set to actually fit a model like this!
Community mixing
Our population lives in two communities, with one larger than the other. They seem to have different mean degrees, as well as some level of assortative mixing. How might we choose to parameterize this?
The first step here is to ask ourselves how many degrees of freedom we have here. We note that:
- In terms of community composition, there are only three types of possible ties in our network: (1,1), (1,2) and (2,2). Note that (2,1) is the same as (1,2) because the ties are undirected.
- Each of these three can be represented by the number of ties of that type. However, the total of these three numbers must add up to our
~edgesterm, which we have already set. - Therefore we only have two degrees of freedom remaining.
We choose to model this with one nodefactor term and one nodematch term, as ~nodefactor("cmty")+nodematch("cmty", diff=FALSE)
The nodefactor term will require one statistic, and produce one coefficient. This is because there are only two values for our community attribute, and nodefactor by default includes an omitted reference category; the default is to omit the value of the attribute that comes first either numerically or alphabetically. For us, that means community 1 will be omitted, and we need to calculate the expected total degree for members of community 2. Our data included 12 community 2 members reporting a total of 8 partnerships, for a mean degree of 8/12 = 0.667. For our simulated population our target stat will be:
For nodematch, we opted to include the argument diff=FALSE, indicating “uniform homophily”. This means there is just one statistic added: the total number of within-community ties, regardless of which community. Using diff=TRUE would have added a statistic for each community; this is called “differential homophily” because it allows different communities to have different tendencies for homophily. However, with only two communities and our other terms set, this is not possible: there is only one degree of freedom remaining, i.e. the homophily level for one community automatically sets the level for the other. Our statistic is thus the total number of within-community ties.
We look again at our data, and count up that 11 of the 17 ties are within-community. So our point estimate for the initial number of within-community ties is
Degree 1
Finally, we want to add in the sex-specific monogamy terms, with degree(1, by = "group")Our two target stats will reflect the expected number of females and males with exactly 1 tie in our initial simulated network.
One might start with the data: 6/10 females and 3/10 males report exactly one tie. In that case, our target stats would be:
However, note that we already decided to change the sex-specific mean degree in our model, relative to our data – the data implied a mean degree of 0.8 for females and 0.9 for males, but we opted for a mean degree of 0.85 for each, given the constraint. Perhaps, then, the sex-specific proportion with one degree also needs to change? Putting it another way, our data had the following degree distributions:
| Degree | 0 | 1 | 2 | mean |
|---|---|---|---|---|
| Females | 30.0% | 60.0% | 10.0% | 0.8 |
| Males | 40.0% | 30.0% | 30.0% | 0.9 |
Changing the mean degree for each but leaving the proportion with degree 1 the same implies the following degree distributions:
| Degree | 0 | 1 | 2 | mean |
|---|---|---|---|---|
| Females | 27.5% | 60.0% | 12.5% | 0.85 |
| Males | 42.5% | 30.0% | 27.5% | 0.85 |
Is that what you want? Perhaps it is. Or perhaps you want to make a different assumption. Image you had a larger data set that had this difference in mean degree, and it wasn’t so easy to attribute it to random sampling variation. Perhaps you have some other reason to think that:
- the (slight) under-reporting on the female side was from women who have 2 partners saying they have 1
- the (slight) over-reporting on the male side was from men who have 0 partners saying they have 1
Then you might want to model the degree distribution as:
| Degree | 0 | 1 | 2 | mean |
|---|---|---|---|---|
| Females | 30.0% | 55.0% | 15.0% | 0.85 |
| Males | 45.0% | 25.0% | 30.0% | 0.85 |
This involves an assumption, and you may feel uncomfortable making such an assumption. But note that keeping the degree 1 statistics straight from the data is a similar assumption about how the other degrees change; it’s just a bit more hidden.
Perhaps you want to model both as a sensitivity analysis, simulating your epidemic in each case to see if your relevant measure of interest changes considerably between the two.
We will proceed with the latter option.
41.2.3 Final formation formula and target stats
Putting all of this together yields:
We then fit the TERGM with the above formula and data, plus a parameterization of a dissolution model with a mean relational duration of 187 time steps.
Finally, we run model diagnostics to ensure the fit is good.
A printing of the mydx object.
EpiModel Network Diagnostics
=======================
Diagnostic Method: Dynamic
Simulations: 25
Time Steps per Sim: 500
Formation Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SE Z Score
edges 850 843.983 -0.708 1.222 -4.925
nodematch.group 0 0.000 NaN NaN NaN
deg3+ 0 0.000 NaN NaN NaN
nodefactor.cmty.2 800 795.641 -0.545 2.300 -1.895
nodematch.cmty 550 544.674 -0.968 1.679 -3.172
deg1.group.1 550 547.108 -0.526 1.143 -2.531
deg1.group.2 250 251.225 0.490 0.825 1.484
SD(Sim Means) SD(Statistic)
edges 9.042 17.285
nodematch.group 0.000 0.000
deg3+ 0.000 0.000
nodefactor.cmty.2 16.490 26.592
nodematch.cmty 13.778 19.859
deg1.group.1 7.046 16.014
deg1.group.2 4.345 12.630
Duration Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means)
edges 187 186.185 -0.436 0.607 -1.343 4.827
SD(Statistic)
edges 6.689
Dissolution Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means)
edges 0.005 0.005 0.297 0 0.719 0
SD(Statistic)
edges 0.002Looks pretty good! We can also confirm with a plot:
If it is of interest, you can also extract the raw data that goes into producing these numerical summaries and plots.
time sim edges nodematch.group deg3+ nodefactor.cmty.2
1 1 1 848 0 0 796
2 2 1 853 0 0 800
3 3 1 853 0 0 796
4 4 1 853 0 0 793
5 5 1 850 0 0 792
6 6 1 854 0 0 792
7 7 1 852 0 0 790
8 8 1 853 0 0 794
9 9 1 850 0 0 793
10 10 1 852 0 0 790
nodematch.cmty deg1.group.1 deg1.group.2
1 568 558 222
2 567 557 221
3 569 555 221
4 570 555 219
5 568 552 222
6 570 552 218
7 568 550 220
8 569 551 219
9 565 554 220
10 568 556 21841.3 Epidemic Simulation
To get the epidemic simulation started, we first need to parameterize the model with epidemic model parameters, initial conditions, and control settings (details provided here).
Code
myparam <- param.net(inf.prob = 0.6, inf.prob.g2 = 0.6,
act.rate = 1.8,
rec.rate = 0.1, rec.rate.g2 = 0.1)
myinit <- init.net(i.num = 100, i.num.g2 = 100)
mycontrol <- control.net("SIS", nsteps = 50, nsims = 5,
nwstats.formula = ~edges + nodematch("cmty") +
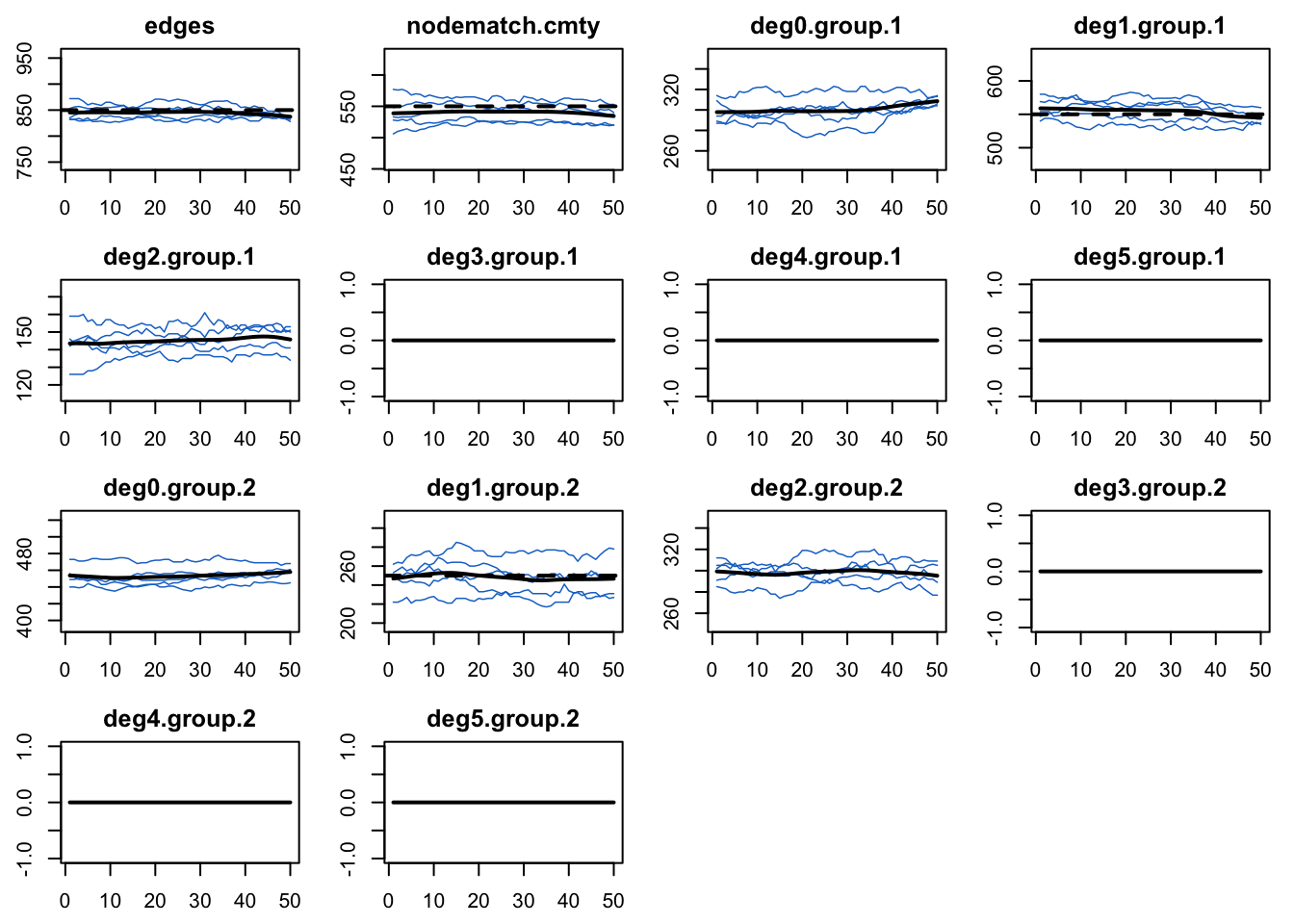
degree(0:5, by = "group"), verbose = TRUE)Noe that we added in some additional degree terms for it to monitor, just to demonstrate that there are indeed no nodes with higher degrees.
Run the epidemic simulation with netsim.
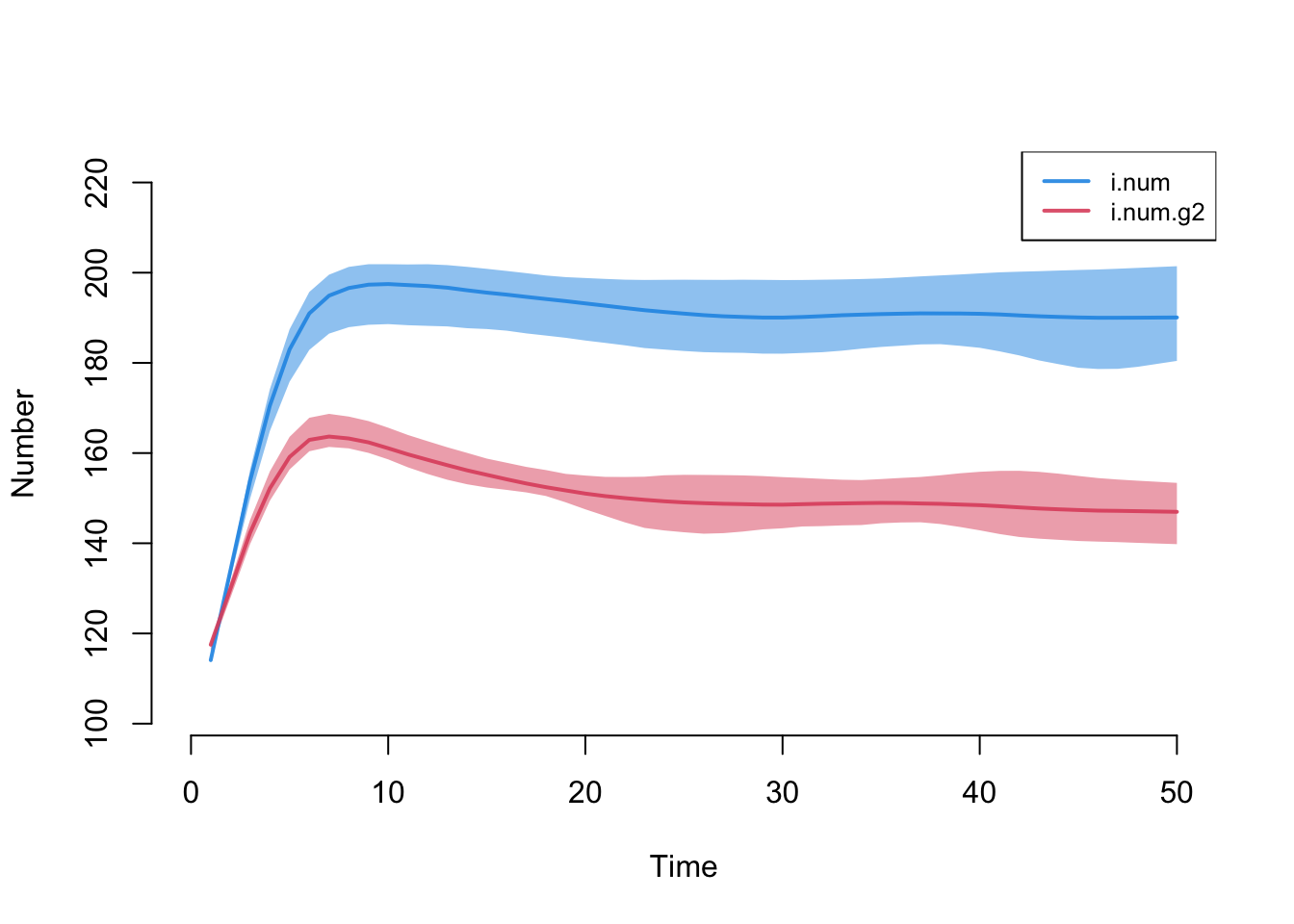
Plot infection prevalence by group. Note that the prevalence in group 1 (females) is higher than group 2 (males). This would once again seem to be driven by the sex-specific differences in concurrency.
Here are numerical summaries for the sex-specific disease prevalence at the final time step.
Code
[1] 0.1904[1] 0.1484We can also calculate and plot network stats as a time series from the epidemic simulations (to ensure that the epidemic simulations did not have unintended consequences on the network structure).