33  Feedback Through Nodal Attribute Changes

This next tutorial will briefly demonstrate how changes to nodal attributes over time are another mechanism that results in feedback between the epidemic system and the dynamic network structure. In the context of diseases like HIV, partnership selection and activity level may vary based on disease status (more specifically, diagnosed disease status but we’ll ignore that complication in this model). Because disease status can change over time, any network model that references the disease status attribute must then be resimulated when the nodal attributes change. And these nodal attributes for disease status change as a function of the infections that results from the network structure. Therefore, we have feedback! This tutorial will walk through the parameterization and implications of this model.

Note

Download the R script to follow along with this tutorial here.

33.1 Network Model

First, we will set up our network and then calculate our target statistics under the parameterization that people with infection have a lower mean degree than those without infection. This may be a function of behavioral change following disease diagnosis, which is commonly observed for HIV. We are not yet considering how they match up.

n <- 500
nw <- network_initialize(n)

33.1.1 Parameterization

The initial prevalence in the network will be 20%. Note that we need to specify a vertex attribute, which must be called status, for this model. This is another “special” attribute on the network, like group, that is treated differently from any other named attribute. That is because status is the main attribute within netsim that keeps track of the individual disease status. We need to initialize the network like this with status as an individual attribute specifically because it will be a term within our TERGM; therefore, we will not randomly set the infected number with init.net as we have in previous tutorials.

Here, we assign exactly 100 nodes as infected, and randomly select which nodes those will be.

prev <- 0.2
infIds <- sample(1:n, n*prev)
nw <- set_vertex_attribute(nw, "status", "s")
nw <- set_vertex_attribute(nw, "status", "i", infIds)
get_vertex_attribute(nw, "status")

  [1] "i" "s" "s" "s" "s" "s" "s" "s" "s" "i" "s" "s" "i" "s" "i" "s" "s" "s"
 [19] "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "i" "s" "s" "s" "i" "s" "s" "s"
 [37] "s" "s" "s" "s" "i" "s" "i" "s" "s" "i" "s" "s" "s" "s" "s" "s" "s" "s"
 [55] "s" "s" "s" "s" "i" "s" "s" "i" "s" "s" "s" "s" "s" "s" "s" "s" "s" "i"
 [73] "s" "s" "s" "i" "s" "s" "s" "s" "s" "s" "i" "s" "i" "s" "s" "s" "i" "i"
 [91] "i" "s" "s" "i" "i" "i" "s" "s" "i" "i" "s" "s" "i" "s" "s" "s" "s" "s"
[109] "s" "s" "i" "s" "s" "s" "i" "s" "s" "i" "s" "s" "s" "i" "s" "s" "s" "s"
[127] "s" "s" "s" "s" "s" "s" "s" "s" "i" "i" "s" "i" "s" "s" "s" "s" "s" "i"
[145] "s" "s" "s" "s" "s" "s" "s" "i" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s"
[163] "s" "s" "s" "s" "s" "s" "s" "s" "i" "s" "i" "s" "i" "s" "i" "i" "s" "s"
[181] "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "i" "s"
[199] "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "i" "s" "s" "s" "s"
[217] "s" "s" "i" "s" "i" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "i" "s"
[235] "s" "i" "s" "s" "s" "s" "s" "s" "s" "s" "i" "i" "s" "s" "s" "i" "i" "s"
[253] "s" "i" "s" "s" "s" "s" "i" "i" "s" "i" "s" "s" "i" "s" "s" "s" "s" "s"
[271] "i" "s" "s" "s" "s" "i" "s" "i" "s" "s" "s" "i" "s" "s" "s" "s" "s" "s"
[289] "i" "s" "i" "s" "i" "s" "i" "s" "s" "s" "s" "s" "s" "i" "s" "i" "s" "s"
[307] "i" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "i"
[325] "s" "s" "s" "i" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "i" "s" "s" "s"
[343] "s" "s" "i" "s" "s" "s" "s" "s" "i" "s" "s" "s" "s" "s" "i" "i" "s" "s"
[361] "s" "s" "i" "s" "s" "s" "s" "s" "s" "i" "s" "s" "i" "i" "s" "s" "s" "s"
[379] "s" "s" "s" "i" "s" "i" "s" "s" "s" "s" "s" "s" "i" "s" "s" "s" "s" "s"
[397] "i" "s" "s" "s" "s" "i" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s"
[415] "i" "s" "s" "s" "s" "s" "s" "s" "s" "s" "i" "i" "s" "i" "s" "s" "s" "i"
[433] "s" "s" "s" "s" "i" "s" "i" "s" "s" "s" "i" "s" "i" "s" "s" "s" "i" "s"
[451] "s" "s" "s" "i" "s" "s" "i" "i" "s" "s" "s" "i" "s" "i" "s" "s" "s" "s"
[469] "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s" "s"
[487] "s" "s" "i" "s" "s" "i" "i" "s" "s" "i" "s" "s" "i" "s"

A nodefactor term will allow the mean degree of the infected persons to differ from that of susceptible persons. In the previous tutorial, we calculated the nodefactor target statistic as the mean degree of a group times the size of the group. Another way of expressing that is a count of the number of times a member of a group, here an infected person or susceptible person, show up in an edge. And this is just the the group mean degree times the group size; here, the group size is defined by the disease prevalence, prev, variable specified above.

mean.deg.inf <- 0.3
inedges.inf <- mean.deg.inf * n * prev
inedges.inf

[1] 30

mean.deg.sus <- 0.8
inedges.sus <- mean.deg.sus * n * (1 - prev)
inedges.sus

[1] 320

The number of edges then is the sum of these two nodefactor statistics divided by 2 (because nodefactor is an expression of nodes).

edges <- (inedges.inf + inedges.sus)/2
edges

[1] 175

Next, let’s move on to parameterizing mixing by disease status. In this theoretically parameterized model, here again it is helpful to think about this in terms of what the expected statistic would be in the absence of any preferential or assortative mixing. That is, what is the value of the nodematch target statistic under a proportional (random) mixing model? We worked this out in the previous tutorial for the case where there were equally sized groups with the same mean degree. It gets more complicated here because the groups are of different sizes, and different activity levels. There are different ways to find this solution.

The exact solution: from population genetics, the Hardy-Weinberg Principle. This code below fills out a two-by-two table that contains the probabilities of a S-S, I-I, and S-I pair. The proportion of partnerships that are matched on status is the diagonal of the table, which is the sum of the S-S and I-I probabilities.

p <- inedges.sus/(edges*2)
q <- 1 - p
nn <- p^2
np <- 2*p*q
pp <- q^2
round(nn + pp, 3)

[1] 0.843

A simulation-based solution: we estimate an ERGM in which there is no nodematch term but heterogeneity in activity, then simulate from that fitted model to calculate the expected number of matched edges. The proportion of matched edges is that number over the total edges.

fit <- netest(nw,
              formation = ~edges + nodefactor("status"),
              target.stats = c(edges, inedges.sus),
              coef.diss = dissolution_coefs(~offset(edges), duration = 1))
sim <- netdx(fit, dynamic = FALSE, nsims = 1e4,
             nwstats.formula = ~edges + nodematch("status"))

Network Diagnostics
-----------------------
- Simulating 10000 networks
- Calculating formation statistics

stats <- get_nwstats(sim)
head(stats)

  sim edges nodefactor.status.s nodematch.status
1   1   197                 364              167
2   2   176                 324              150
3   3   205                 377              172
4   4   174                 322              148
5   5   172                 322              150
6   6   181                 328              151

round(mean(stats$nodematch.status/stats$edges), 3)

[1] 0.843

The main substantive finding here is that 84% of relations are expected to be within the same disease status group under a proportional mixing group, even without a behavioral preference for assortative mixing. This is because suceptible persons are a larger group in the population, and have more relationships per-capita.

Let us now imagine that there are in fact slightly more within-group ties than expected by chance:

nmatch <- edges * 0.91

33.1.2 Estimation

This tutorial will compare two models to assess the impact of behavior driven by disease status on epidemic trajectories:

• Model 1 features two forms of seroadaptive behavior: different levels of activity by disease status, and matching on status.
• Model 2 has neither, so is just a Bernoulli model with same mean degree as Model 1.

33.1.2.1 Model 1

The network model with serosorting will include terms for both the number of times susceptible persons show up in an edge, as well as the number of node-matched edges overall. It is unnecessary to specify the nodefactor term for the susceptible persons because that is a function of total edges and the nodefactor term for the infected persons (the base level is always the first in alphabetical or numerical order, so “i” for our status variable level in this case). The average partnership duration in both models will be 50 time steps.

formation <- ~edges + nodefactor("status") + nodematch("status")
target.stats <- c(edges, inedges.sus, nmatch)

coef.diss <- dissolution_coefs(dissolution = ~offset(edges), 50)

est <- netest(nw, formation, target.stats, coef.diss)

Warning: 'glpk' selected as the solver, but package 'Rglpk' is not available;
falling back to 'lpSolveAPI'. This should be fine unless the sample size and/or
the number of parameters is very big.

We run the network diagnostics on the model.

dx <- netdx(est, nsims = 10, nsteps = 500, ncores = 5,
            nwstats.formula = ~edges + 
                               meandeg + 
                               nodefactor("status", levels = NULL) + 
                               nodematch("status"), verbose = FALSE)
dx

EpiModel Network Diagnostics
=======================
Diagnostic Method: Dynamic
Simulations: 10
Time Steps per Sim: 500

Formation Diagnostics
----------------------- 
                    Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means)
edges               175.00  172.694   -1.318  1.784  -1.293         6.270
meandeg                 NA    0.691       NA  0.007      NA         0.025
nodefactor.status.i     NA   30.193       NA  0.802      NA         1.901
nodefactor.status.s 320.00  315.195   -1.502  3.212  -1.496        12.217
nodematch.status    159.25  156.651   -1.632  1.778  -1.462         6.522
                    SD(Statistic)
edges                      14.772
meandeg                     0.059
nodefactor.status.i         6.567
nodefactor.status.s        27.327
nodematch.status           14.541

Duration Diagnostics
----------------------- 
      Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
edges     50   50.168    0.336  0.455   0.369          1.75         3.909

Dissolution Diagnostics
----------------------- 
      Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
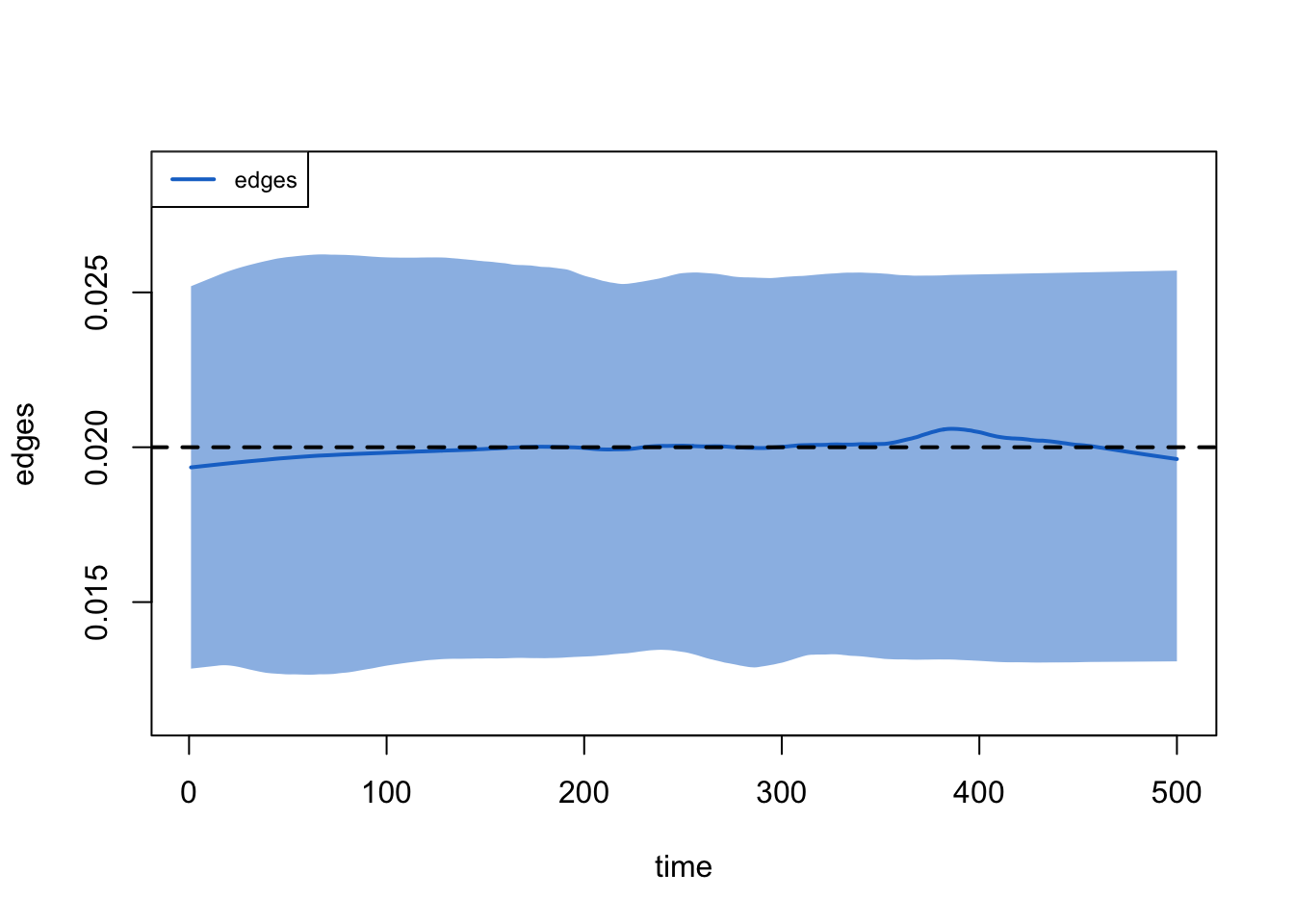
edges   0.02     0.02   -0.057      0  -0.074             0         0.011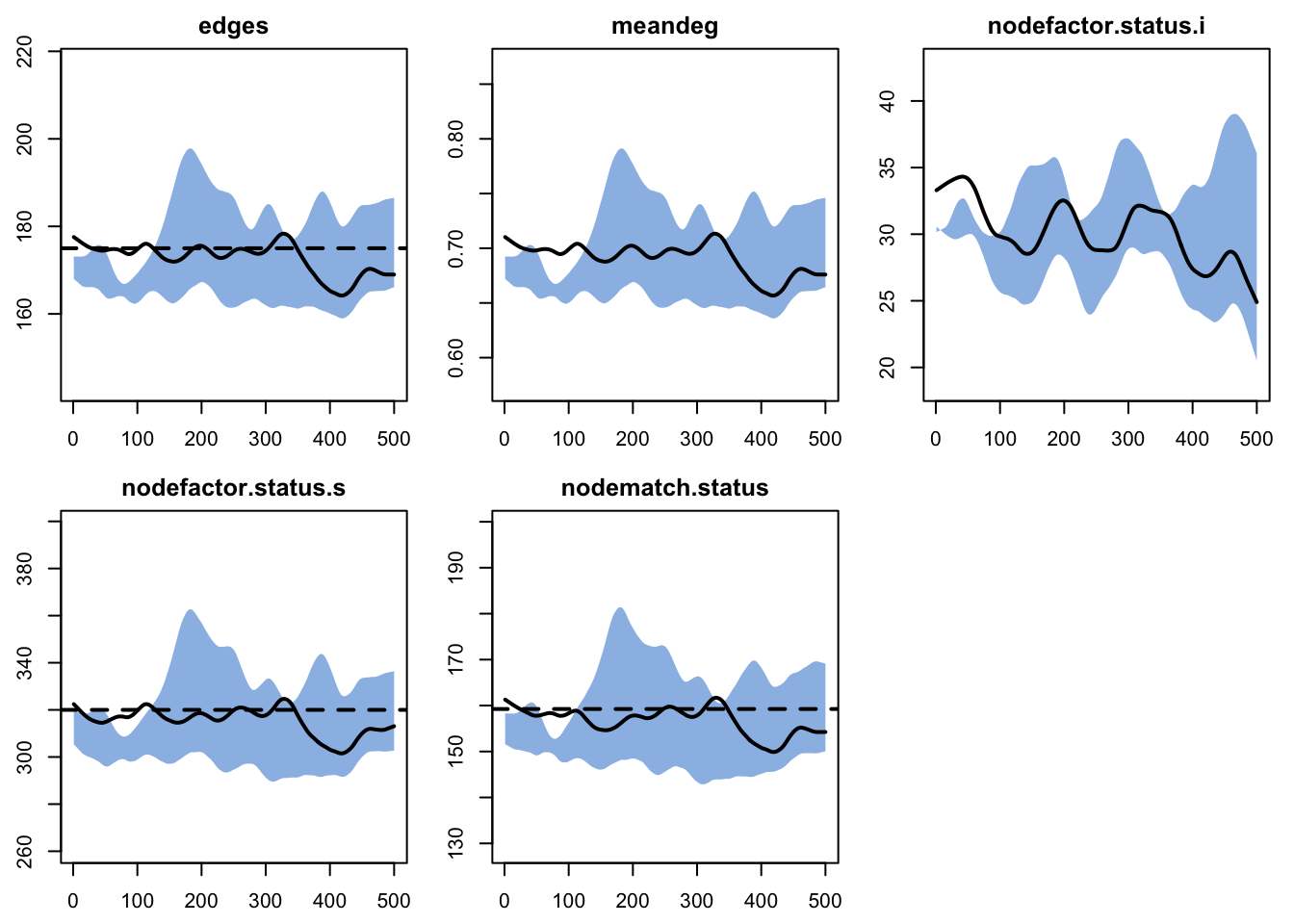

plot(dx)

plot(dx, type = "dissolution")

33.1.2.2 Model 2

The second model will include only an edges term, so no serosorting behavior but same amount of activity among nodes. We are recycling the nw object with the status attribute set from above.

est2 <- netest(nw, formation = ~edges, target.stats = edges, coef.diss)

After estimation, the diagnostics here look fine too. Compare the nodefactor and nodematch simulations here to those in the Model 1 diagnostics: more edges for infected persons, and more discordant (S-I) edges.

dx2 <- netdx(est2, nsims = 10, nsteps = 1000, ncores = 5,
             nwstats.formula = ~edges + 
                                meandeg + 
                                nodefactor("status", levels = NULL) + 
                                nodematch("status"), verbose = FALSE)
dx2

EpiModel Network Diagnostics
=======================
Diagnostic Method: Dynamic
Simulations: 10
Time Steps per Sim: 1000

Formation Diagnostics
----------------------- 
                    Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means)
edges                  175  175.724    0.414  1.065    0.68         4.082
meandeg                 NA    0.703       NA  0.004      NA         0.016
nodefactor.status.i     NA   71.305       NA  0.815      NA         2.540
nodefactor.status.s     NA  280.143       NA  1.942      NA         6.932
nodematch.status        NA  119.304       NA  0.963      NA         2.917
                    SD(Statistic)
edges                      12.724
meandeg                     0.051
nodefactor.status.i         9.124
nodefactor.status.s        22.209
nodematch.status           11.021

Duration Diagnostics
----------------------- 
      Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
edges     50   49.916   -0.168  0.293  -0.287         0.904         3.511

Dissolution Diagnostics
----------------------- 
      Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
edges   0.02     0.02   -0.462      0  -0.922             0          0.01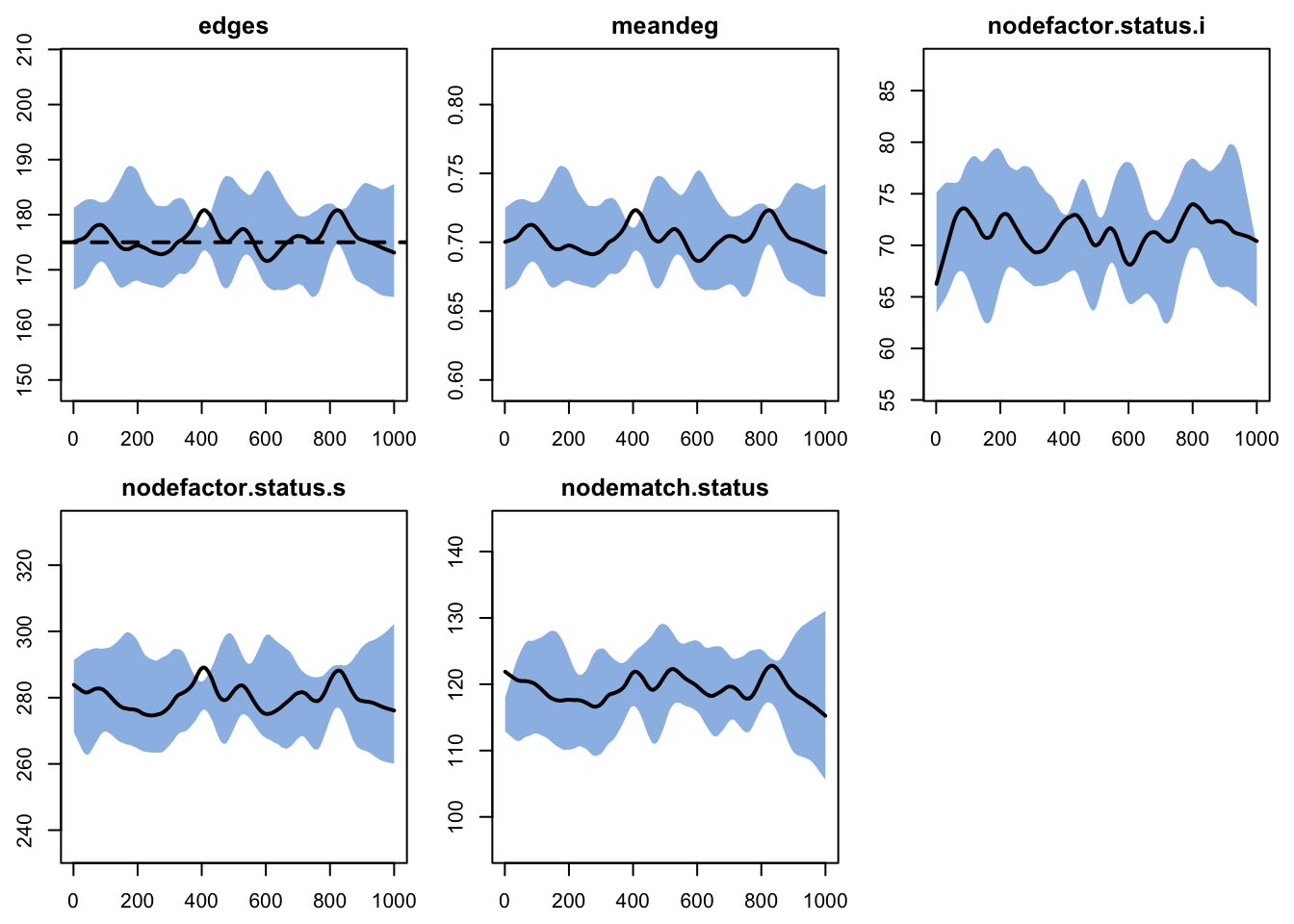

plot(dx2)

33.2 Epidemic Model

For the epidemic model, we will simulate an SI disease, with our two counterfactual network models. The first model will use the serosorting network model, and the second will be the random Bernoulli model.

33.2.1 Model 1

The model will only include one named parameter, for the transmission probability per contact.

param <- param.net(inf.prob = 0.03)

The initial conditions are now passed through to the epidemic model not through init.net as with previous examples, but through the netest object that contains the original starting network with the vertex attributes for status. However, because netsim will still be expecting an initial conditions list, we need to create an empty object as a placeholder.

init <- init.net()

For the control settings, we monitor the same network statistics as we did in the network diagnostics above. The resimulate.networks argument must be set to TRUE because the network needs to be updated at each time step. In this model, we will use the tergmLite approach since we do not need to monitor individual-level network histories.

control <- control.net(type = "SI", nsteps = 500, nsims = 5, ncores = 5,
                       resimulate.network = TRUE, tergmLite = TRUE,
                       nwstats.formula = ~edges + 
                                          meandeg + 
                                          nodefactor("status", levels = NULL) + 
                                          nodematch("status"))

Here, we run the model. We will return to it to compare output later.

sim <- netsim(est, param, init, control)

33.2.2 Model 2

The second model includes the same epidemic parameters as Model 1, so all that we need to change is the first parameter for the different network object.

sim2 <- netsim(est2, param, init, control)

33.2.3 Results

Here we’ll look at the epidemic results first and then the network diagnostics, because the network statistics will be a function of the epidemiology.

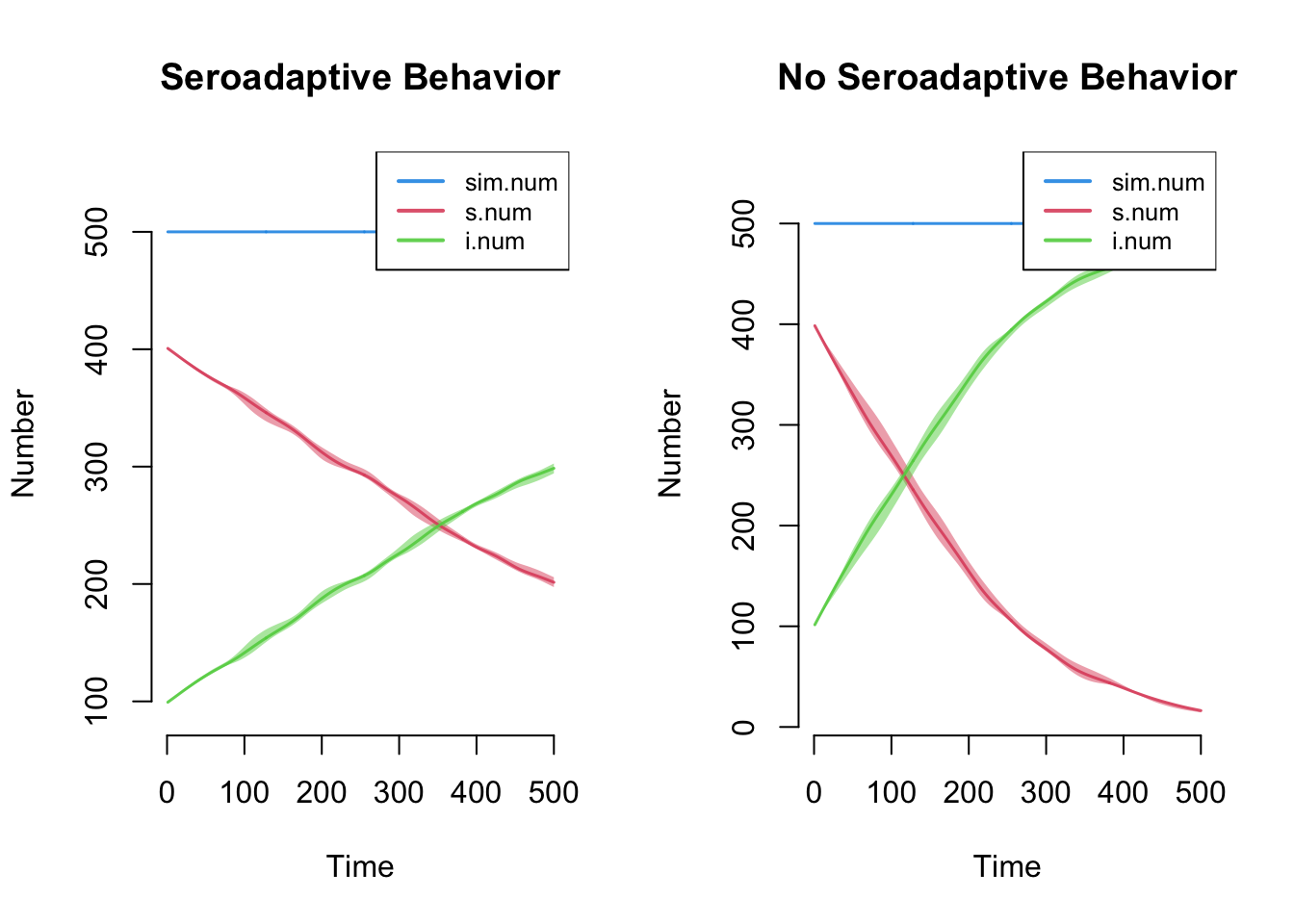
Here we see that the serosorting model grows much less quickly than the random model. The reasons are that nodes lower their mean degree upon infection, and therefore have fewer partners over time. They also tend to preferentially partner with other infecteds.

par(mfrow = c(1,2))
plot(sim, main = "Seroadaptive Behavior")
plot(sim2, main = "No Seroadaptive Behavior")

Another method to show the relative difference is to plot the two epidemic trajectories together. This requires a custom legend.

par(mfrow = c(1,1))
plot(sim, y = "i.num", popfrac = TRUE, sim.lines = FALSE, qnts = 1)
plot(sim2, y = "i.num", popfrac = TRUE, sim.lines = FALSE, qnts = 1, 
     mean.col = 2, qnts.col = 2, add = TRUE)
legend("topleft", c("Serosort", "Non-Serosort"), lty = 1, lwd = 3,
       col = c(4, 2), cex = 0.9, bty = "n")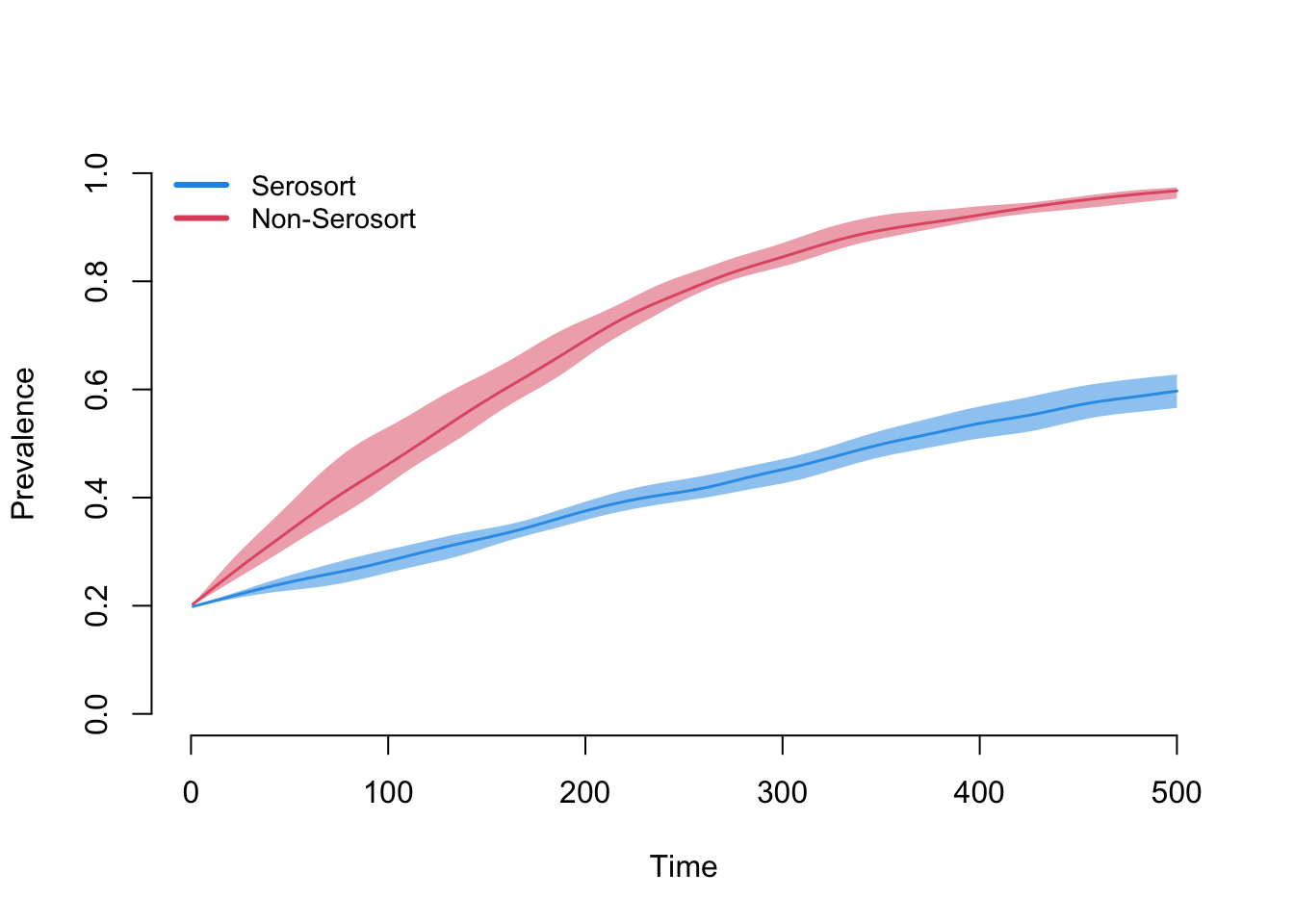

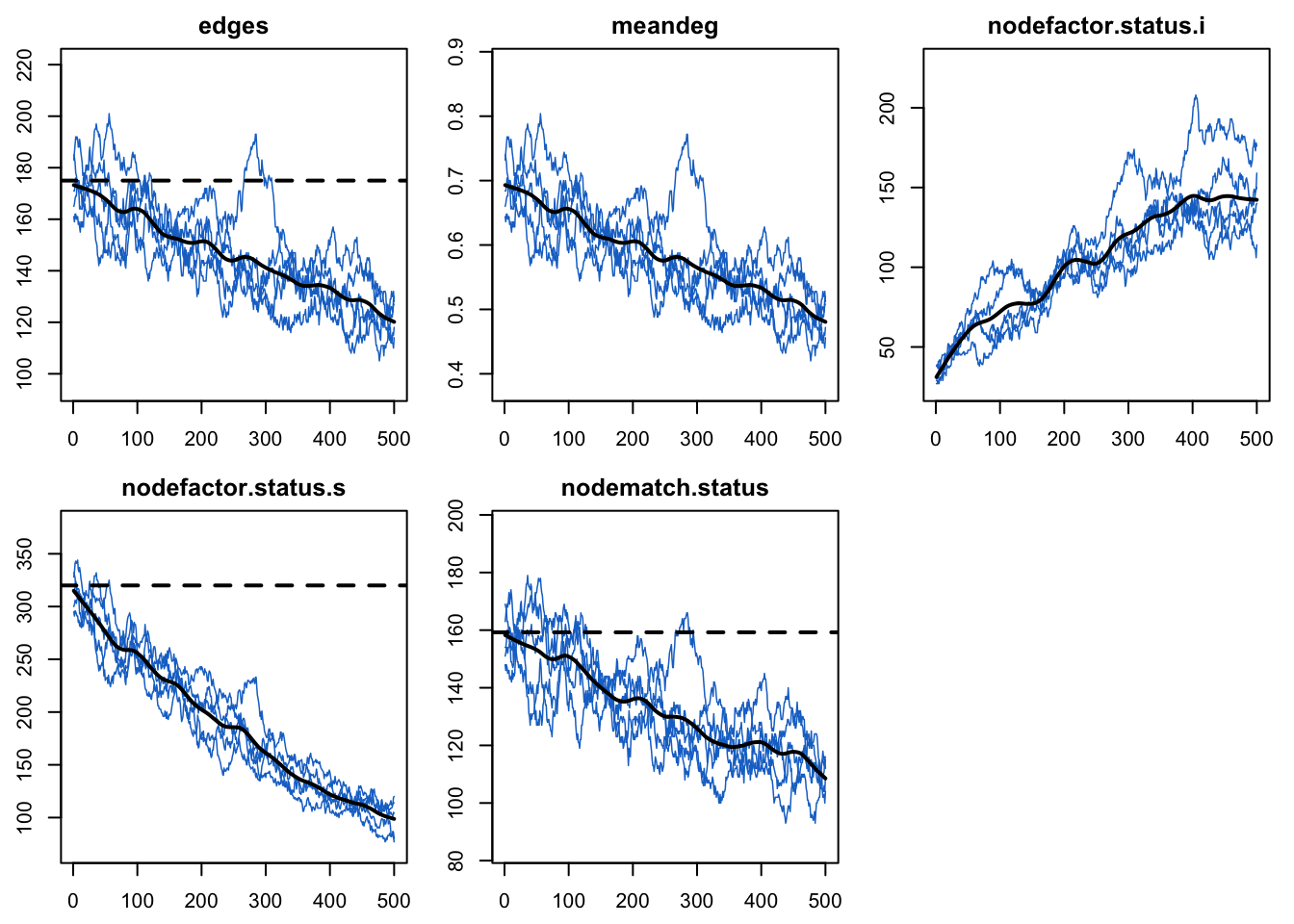
Now, here are the network statistics that we monitored in Model 1. In contrast to our previous tutorials, where we expected stochastic variation around the targets to be preserved over time, here every network statistic varies.

plot(sim, type = "formation", qnts = FALSE, sim.lines = TRUE)

Notice first that the nodefactor statistics are moving in opposite directions: as the prevalence of disease increases from 20% to approximately 50% at time 500, the number of infected nodes in an edge increases. The quantity preserved is not the number of infected nodes in an edge that we set as a target (30 nodes); rather, it is the log-odds of an infected node in an edge conditional on other terms in the model.

plot(sim, type = "formation", qnts = FALSE, sim.lines = TRUE,
     stats = c("nodefactor.status.s", 
               "nodefactor.status.i"))

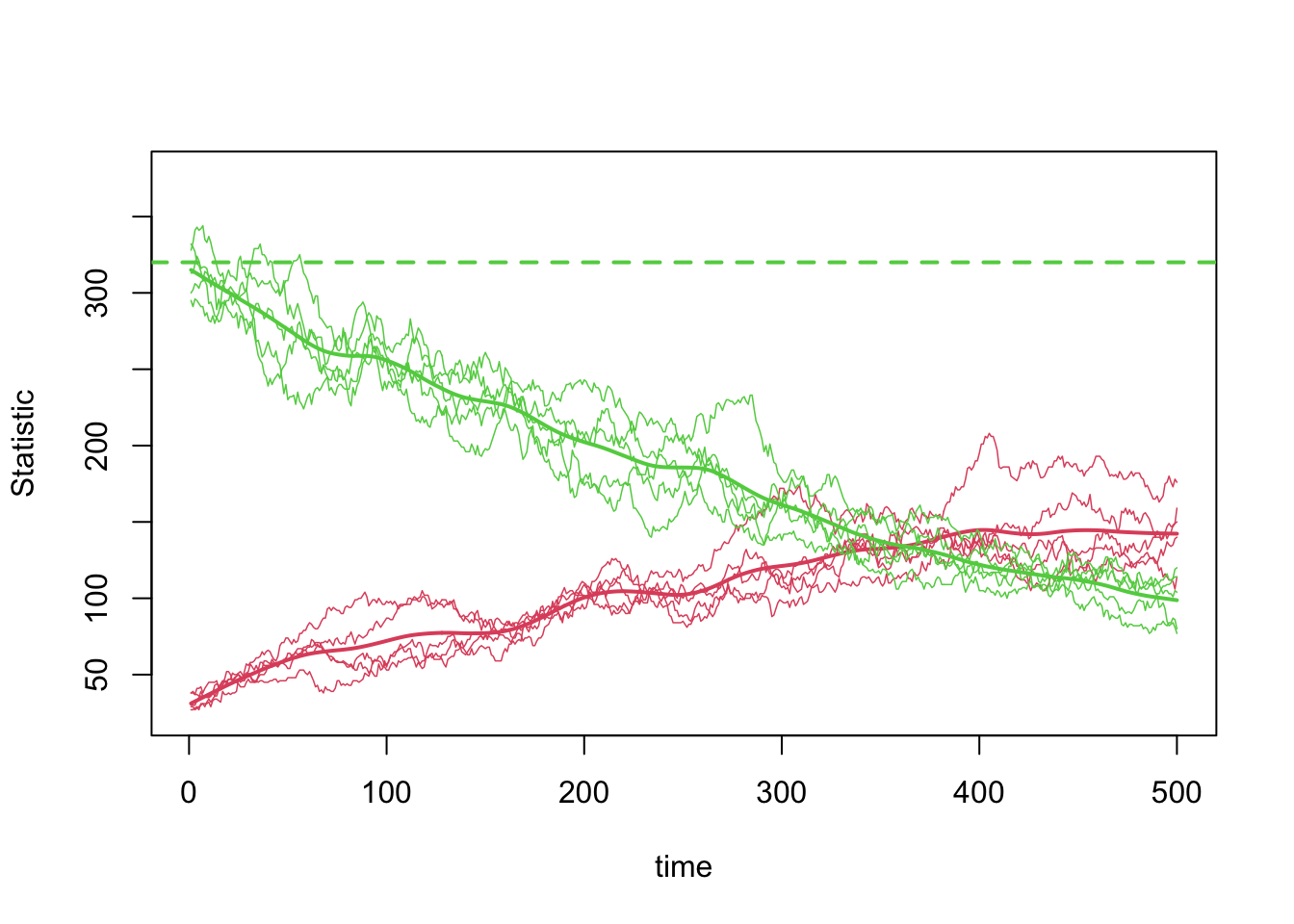
Second, note that the total edges and node-matched edges decline over time. This plot shows those two statistics from one simulation only for clarity. Ordinarily the mean degree is preserved even in a population with drastically changing size, due to the network density correction that automatically occurs in netsim.

plot(sim, type = "formation", 
     stats = c("edges", "nodematch.status"), 
     qnts = FALSE, sims = 1, sim.lwd = 2)

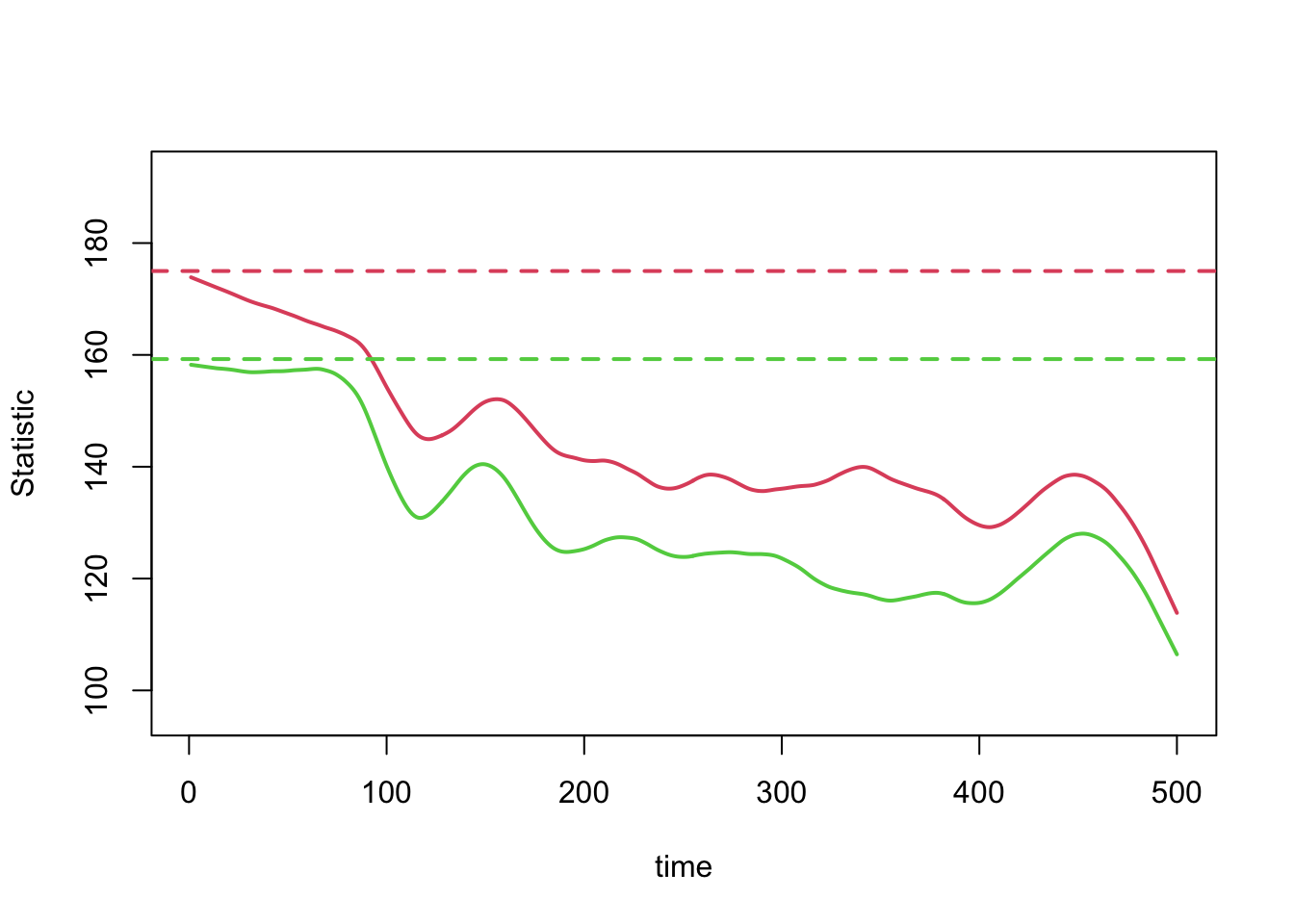
But in this case, the edges and mean degree are shrinking because the number of nodes in the network with the same status is steadily increasing, which draws the node match statistic lower since there are fewer susceptible-susceptible pairs available. Since the edges is a constant multiple of node-matched edges, they move together.

After looking at so many models where the target statistics were preserved throughout the simulation, this may seem like odd or undesirable behavior here. If it does, think about the main assumption we began with: men who are infected tend to have lower rates of partnering than men who are not infected. Perhaps this is because they are ill, or because they are trying to protect others. If this is the case, then what should we expect to happen to the overall rate of partnering as the proportion of men who are infected increases? Presumably it should go down, which is precisely what we see.

This behavior does mean that it can be difficut to tease apart the different contributions of serosorting to the disease dynamics that we see. How much of serosorting’s effect on lowering transmission came from the rate of overall partner reductions for infected men, and how much came from the homophily effect where infected men partner with each other relatively more? Although we included both in our model (through the nodefactor and nodematch terms, respectively), one could easily consider intermediate models that only included one term or the other, and then compare the results of each to the two models we already considered. We would then have a sense of the individual effects of each of these behavioral components, as well as their combined effect. Is the latter additive, less than additive, or more than additive (i.e. synergistic?)