library(EpiModel)
rm(list = ls())39 Adding Demography to COVID Model
In this tutorial, we will build on our SEIR model for COVID-19 by adding demography (aging, births, and deaths). This will involve learning a few new components of the EpiModel extension API.
39.1 Setup
First start by loading EpiModel and clearing your global environment.
We will use the extension infection and disease progression modules from Day 4. Like the models with extension modules we ran then, we will keep the functions within one R script and the code to run the model in another script. For the purposes of this tutorial, we will show them bundled together but the linked files are split.
We will start with the initialization of the network object, with the relevant age and disease status attributes, then show the new epidemic models, then the network model estimation, and then epidemic model parameterization and simulation. In practice, we would typically go back and forth many times between all of these components.
39.2 Network Initialization
The model will represent age as a continuous nodal attribute. Aging will increment this attribute for everyone by a day (the value of the time step) in a linear fashion, and mortality will be a function of age.
To start, we initialize the range of possible ages (in years) at the outset.
ages <- 0:85Next, we calculate age-specific mortality rates based on one demographic table online. This lists the rates per year per 100,000 persons in the United States by age groups, in the following age bands:
# Rates per 100,000 for age groups: <1, 1-4, 5-9, 10-14, 15-19, 20-24, 25-29,
# 30-34, 35-39, 40-44, 45-49, 50-54, 55-59,
# 60-64, 65-69, 70-74, 75-79, 80-84, 85+
departure_rate <- c(588.45, 24.8, 11.7, 14.55, 47.85, 88.2, 105.65, 127.2,
154.3, 206.5, 309.3, 495.1, 736.85, 1051.15, 1483.45,
2294.15, 3642.95, 6139.4, 13938.3)To convert this to a per-capita daily death rate, we divide by 365,000:
dr_pp_pd <- departure_rate / 1e5 / 365Next we build out a vector of daily death rates by repeating the rate above by the size of the age band. Now we have a rate for each age, with some repeats within age band.
age_spans <- c(1, 4, rep(5, 16), 1)
dr_vec <- rep(dr_pp_pd, times = age_spans)
head(data.frame(ages, dr_vec), 20) ages dr_vec
1 0 1.612192e-05
2 1 6.794521e-07
3 2 6.794521e-07
4 3 6.794521e-07
5 4 6.794521e-07
6 5 3.205479e-07
7 6 3.205479e-07
8 7 3.205479e-07
9 8 3.205479e-07
10 9 3.205479e-07
11 10 3.986301e-07
12 11 3.986301e-07
13 12 3.986301e-07
14 13 3.986301e-07
15 14 3.986301e-07
16 15 1.310959e-06
17 16 1.310959e-06
18 17 1.310959e-06
19 18 1.310959e-06
20 19 1.310959e-06It ends up looking like this visually:
par(mar = c(3,3,2,1), mgp = c(2,1,0), mfrow = c(1,1))
plot(ages, dr_vec, type = "o", xlab = "age", ylab = "Mortality Rate")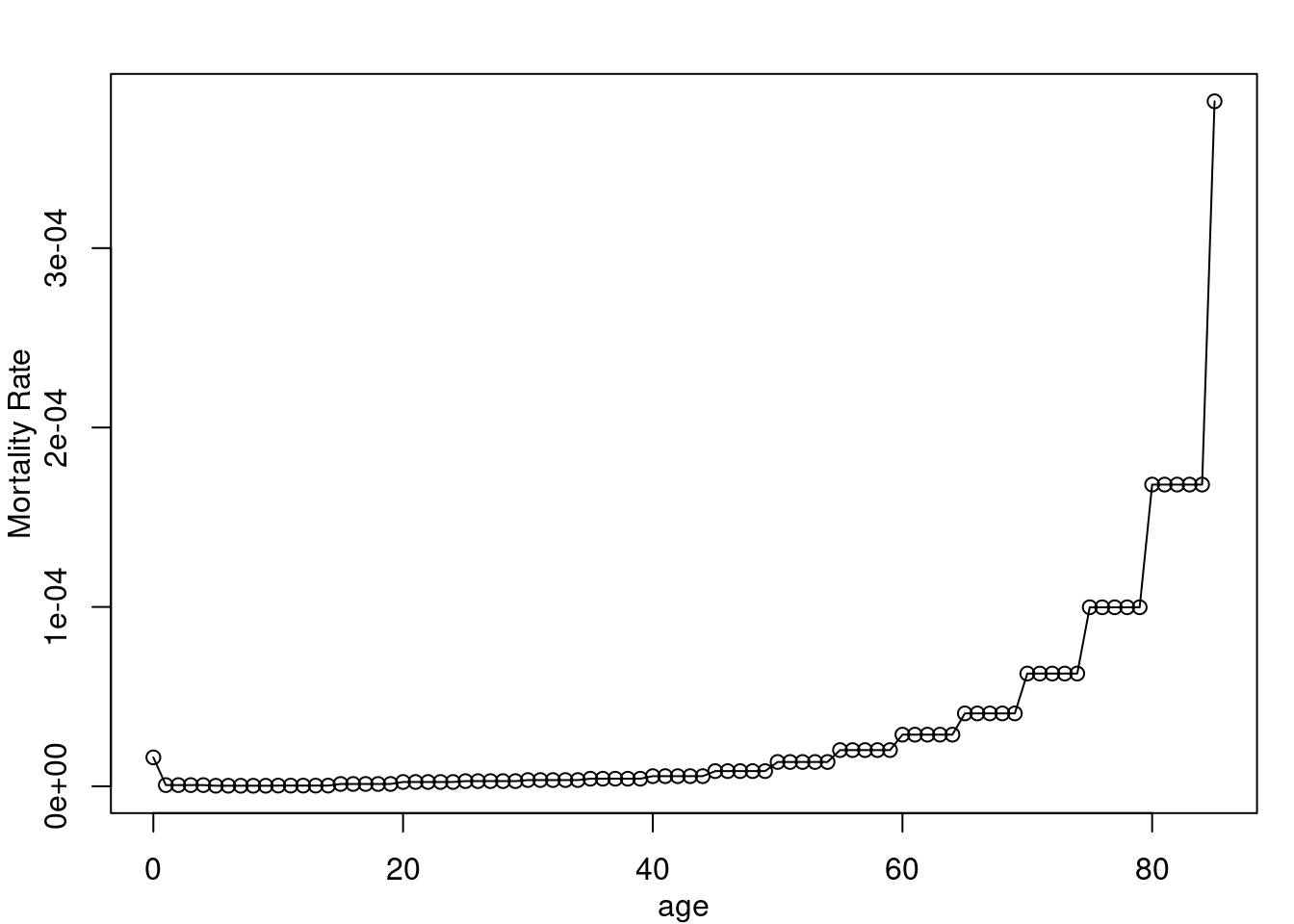
We will now add age and disease status attributes to an initialized network object. We will use a larger population size than last time:
n <- 1000
nw <- network_initialize(n)For each node, we will randomly sample an age from the vector of ages (from 0 to 85), and then set that as a vertex attribute on the network object.
ageVec <- sample(ages, n, replace = TRUE)
nw <- set_vertex_attribute(nw, "age", ageVec)This model will also initialize people into a latent (E state) disease stage.
statusVec <- rep("s", n)
init.latent <- sample(1:n, 50)
statusVec[init.latent] <- "e"
table(statusVec)statusVec
e s
50 950 which(statusVec == "e") [1] 20 21 36 74 88 116 153 155 169 175 177 183 190 197 276 288 320 325 330
[20] 364 402 412 414 421 427 461 479 489 520 531 558 566 571 641 660 663 669 677
[39] 684 733 734 738 769 810 852 855 866 900 902 962Because of that we will manually set up a vector of disease statuses and set it on the network object as a status attribute. This is an alternative way to set up disease status, instead of using the initial conditions in init.net.
nw <- set_vertex_attribute(nw, "status", statusVec)
nw Network attributes:
vertices = 1000
directed = FALSE
hyper = FALSE
loops = FALSE
multiple = FALSE
bipartite = FALSE
total edges= 0
missing edges= 0
non-missing edges= 0
Vertex attribute names:
age status vertex.names
No edge attributes39.3 Demographic Modules
With the network initialized, we will now turn to building out the three new extension modules. This set of extensions will add three demographic processes to the model: aging, births, and deaths. The birth and death processes in particular will involve some specific changes to the nodes that must be completed under the EpiModel extension API.
39.3.1 Aging
The aging module performs one simple process: to update the age attribute (in years) of everyone on the network by a day (or 1/365 years). It does this by getting the age attribute from the dat object, updating the vector, and then setting it back on the dat object. The function design follows the same format as our SEIR modules in Day 4.
aging <- function(dat, at) {
age <- get_attr(dat, "age")
age <- age + 1/365
dat <- set_attr(dat, "age", age)
dat <- set_epi(dat, "meanAge", at, mean(age, na.rm = TRUE))
return(dat)
}We also add a new summary statistic, meanAge, which is the mean of the age vector for that time step.
39.3.2 Mortality
For the mortality module, we will implement a process of age-specific mortality with an excess risk of death with active infection. The process is more complex than the built-in departures module (which might cover death but other forms of exit from the population). We will step through the function together in the tutorial.
Note that the overall design of the function is similar to any other EpiModel extension module. The get_ and set_ functions are used to read and write to the dat object. The individual process of mortality involves querying the death rates by the age of active nodes, and then drawing from a binomial distribution for each eligible node.
EpiModel API Rule: For nodes who have died, two specific nodal attributes must be updated: active and exitTime. Upon death, the active value of those nodes turns from 1 to 0. The exitTime is the current time step, at. These two nodal attributes must be updated in a death (or other departure) module to tell EpiModel how to appropriately update the network object at the end of the time step (which you never have to worry about).
dfunc <- function(dat, at) {
## Attributes
active <- get_attr(dat, "active")
exitTime <- get_attr(dat, "exitTime")
age <- get_attr(dat, "age")
status <- get_attr(dat, "status")
## Parameters
dep.rates <- get_param(dat, "departure.rates")
dep.dis.mult <- get_param(dat, "departure.disease.mult")
## Query alive
idsElig <- which(active == 1)
nElig <- length(idsElig)
## Initialize trackers
nDepts <- 0
idsDepts <- NULL
if (nElig > 0) {
## Calculate age-specific departure rates for each eligible node ##
## Everyone older than 85 gets the final mortality rate
whole_ages_of_elig <- pmin(ceiling(age[idsElig]), 86)
drates_of_elig <- dep.rates[whole_ages_of_elig]
## Multiply departure rates for diseased persons
idsElig.inf <- which(status[idsElig] == "i")
drates_of_elig[idsElig.inf] <- drates_of_elig[idsElig.inf] *
dep.dis.mult
## Simulate departure process
vecDepts <- which(rbinom(nElig, 1, drates_of_elig) == 1)
idsDepts <- idsElig[vecDepts]
nDepts <- length(idsDepts)
## Update nodal attributes
if (nDepts > 0) {
active[idsDepts] <- 0
exitTime[idsDepts] <- at
}
}
## Set updated attributes
dat <- set_attr(dat, "active", active)
dat <- set_attr(dat, "exitTime", exitTime)
## Summary statistics ##
dat <- set_epi(dat, "total.deaths", at, nDepts)
# covid deaths
covid.deaths <- length(intersect(idsDepts, which(status == "i")))
dat <- set_epi(dat, "covid.deaths", at, covid.deaths)
return(dat)
}Note that the overall process of mortality involves flipping a coin for each eligible person in the population, weighted by their age and disease status, and keeping track of who came up as heads (i.e., a 1). We end the function by saving two summary statistics that count the overall deaths and the COVID-related deaths separately.
39.3.3 Births
Finally, we add a new arrivals module to handle births (there may be other forms of arrivals such as in-migration that we would like to handle separately) but not in this model. In terms of the process, births is a simple function of the current population size times a fixed birth rate. This is stochastic at each time step by drawing an non-negative integer from a Poisson distribution.
EpiModel API Rule: If there are any births, then all the nodal attributes for incoming nodes must be specified. At a minimum, all EpiModel models must have these 5 attributes: active, status, infTime, entrTime, and exitTime. The append_core_attr function automatically handles the updating of the active, entrTime, and exitTime attributes, since these will be uniform across models. Users are responsible for updating status and infTime with the desired incoming values, using the append_attr function. Any other nodal attributes specific to your model, such as age in our current model, should also be appended using this approach. The append_attr function allows you to write those standard values to the end of the attribute vectors, where new nodes are “placed” in terms of their position on the vector. append_attr can either take a single value (repeated for all new arrivals) or a vector of values that may be unique for each arrival.
afunc <- function(dat, at) {
## Parameters ##
n <- get_epi(dat, "num", at - 1)
a.rate <- get_param(dat, "arrival.rate")
## Process ##
nArrivalsExp <- n * a.rate
nArrivals <- rpois(1, nArrivalsExp)
# Update attributes
if (nArrivals > 0) {
dat <- append_core_attr(dat, at = at, n.new = nArrivals)
dat <- append_attr(dat, "status", "s", nArrivals)
dat <- append_attr(dat, "infTime", NA, nArrivals)
dat <- append_attr(dat, "age", 0, nArrivals)
}
## Summary statistics ##
dat <- set_epi(dat, "a.flow", at, nArrivals)
return(dat)
}We close the function by adding a summary statistic for the number of births.
39.4 Network Model Estimation
With the new modules defined, we can return to parameterizing the network model. Recall that we have initialized the network and set the age and status attributes on the network above.
nw Network attributes:
vertices = 1000
directed = FALSE
hyper = FALSE
loops = FALSE
multiple = FALSE
bipartite = FALSE
total edges= 0
missing edges= 0
non-missing edges= 0
Vertex attribute names:
age status vertex.names
No edge attributesNext we will parameterize the model starting with the same terms as our last SEIR model, but adding an absdiff term for age. This will control the average absolute difference in ages between any two nodes. With a small target statistic, this will allow for continuous age homophily (assortative mixing).
formation <- ~edges + degree(0) + absdiff("age")For target statistics, we will start with mean degree, transform that to the expected edges, and then calculate the number of isolates (a synonym for degree(0)) as a proportion of nodes, and absdiff as a function of edges (the target statistic is the sum of all absolute differences in age across all edges, so this is the mean difference times the number of edges).
mean_degree <- 2
edges <- mean_degree * (n/2)
avg.abs.age.diff <- 2
isolates <- n * 0.08
absdiff <- edges * avg.abs.age.diff
target.stats <- c(edges, isolates, absdiff)
target.stats[1] 1000 80 2000The dissolution model will use a standard homogeneous dissolution rate, with a death correction here based on the average death rate across the population and a multiplier to account for higher mortality due to COVID. This is not perfect, but this parameter is quite robust to misspecification because the huge differential in average relational duration versus average lifespan (1/mortality rates); notice the minimal change in coefficient with this adjustment.
coef.diss <- dissolution_coefs(~offset(edges), 20, mean(dr_vec)*2)
coef.dissDissolution Coefficients
=======================
Dissolution Model: ~offset(edges)
Target Statistics: 20
Crude Coefficient: 2.944439
Mortality/Exit Rate: 6.31841e-05
Adjusted Coefficient: 2.946969Next we fit the model. You can ignore any warning messages about fitted probabilities that were 0 or 1. These are standard GLM fitting messages. If there is a problem in the model fit, it will emerge in the diagnostics.
est <- netest(nw, formation, target.stats, coef.diss)We will run the model diagnostics by monitoring both the terms in the model formula and an extension of the degree terms out to degree of 6. We are using an MCMC control setting here to tweak the simulation algorithm to increase the “burn-in” for the Markov chain; this burn-in control is especially helpful in cases of ERGM formulas with absdiff terms (i.e., those with continuous attributes). Although the fit is not perfect here (we are on the cusp of where we also might want to turn off the edges dissolution approximation with edapprox), it is close enough to move forward for this tutorial.
dx <- netdx(est, nsims = 10, ncores = 5, nsteps = 500,
nwstats.formula = ~edges + absdiff("age") + degree(0:6),
set.control.tergm = control.simulate.formula.tergm(MCMC.burnin.min = 20000))
Network Diagnostics
-----------------------
- Simulating 10 networks
- Calculating formation statisticsprint(dx)EpiModel Network Diagnostics
=======================
Diagnostic Method: Dynamic
Simulations: 10
Time Steps per Sim: 500
Formation Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
edges 1000 988.485 -1.151 2.134 -5.396 6.427 28.297
absdiff.age 2000 1979.000 -1.050 6.337 -3.314 27.847 84.996
degree0 80 88.144 10.180 0.455 17.893 2.134 10.212
degree1 NA 321.354 NA 0.781 NA 4.430 16.452
degree2 NA 292.968 NA 0.593 NA 2.339 14.906
degree3 NA 176.649 NA 0.466 NA 2.449 12.546
degree4 NA 79.955 NA 0.387 NA 1.307 9.298
degree5 NA 29.264 NA 0.246 NA 0.698 5.759
degree6 NA 8.841 NA 0.110 NA 0.381 3.062
Duration Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
edges 20 20.057 0.284 0.055 1.035 0.192 0.657
Dissolution Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
edges 0.05 0.05 -0.147 0 -0.757 0 0.007plot(dx)
39.5 EpiModel Model Simulation
To parameterize the model, we need to add the newly referenced model parameters to param.net. These include the departure and arrival rates. Although our past parameters have been scalars (single values), there is nothing to prevent us from passing vectors (or even more structured objects like lists or data frames) as parameters. That is what we do with departure.rates. The departure.disease.mult is the multiplier on the base death rate for persons with active infection (persons in the “i” status). We will assume the arrival rate reflects the average lifespan in days.
param <- param.net(inf.prob = 0.1,
act.rate = 3,
departure.rates = dr_vec,
departure.disease.mult = 100,
arrival.rate = 1/(365*85),
ei.rate = 0.05, ir.rate = 0.05)For initial conditions, we have passed in the number initially in the latent state at the outset, so init.net just needs to be a placeholder input.
init <- init.net()Finally, for control settings, we first source in the new function script (this should now contain five extension functions), and include module names and associated functions for each of the five. Note that these five modules will run in addition to the standard modules that handle initialization, network resimulation, and so on. For this model, we definitely want to resimulate the network at each time step, and we will use tergmLite for computational efficiency. We again use a burn-in control setting for TERGM simulations here, plus add some additional network statistics to monitor for diagnostics.
source("d5-s4-COVIDDemog-fx.R")
control <- control.net(type = NULL,
nsims = 5,
ncores = 5,
nsteps = 300,
infection.FUN = infect,
progress.FUN = progress,
aging.FUN = aging,
departures.FUN = dfunc,
arrivals.FUN = afunc,
resimulate.network = TRUE,
tergmLite = TRUE,
set.control.tergm = control.simulate.formula.tergm(MCMC.burnin.min = 10000),
nwstats.formula = ~edges + meandeg + degree(0:2) + absdiff("age"))With all that complete, we now are ready to run netsim. This should take a minute.
sim <- netsim(est, param, init, control)39.6 Post-Simulation Diagnostics
We run the network diagnostics with the netsim simulations complete to evaluate the potential impact of the epidemic processes on the network diagnostics. Here we see that the three targeted statistics are not maintained at their target levels. Part of this may be due to the general bias in the fit introduced by the edges dissolution approximation, highlighted in the netdx diagnostics above. But the change to the edges and absdiff statistics may be concerning.
plot(sim, type = "formation",
stats = c("edges", "absdiff.age", "degree0"), plots.joined = FALSE)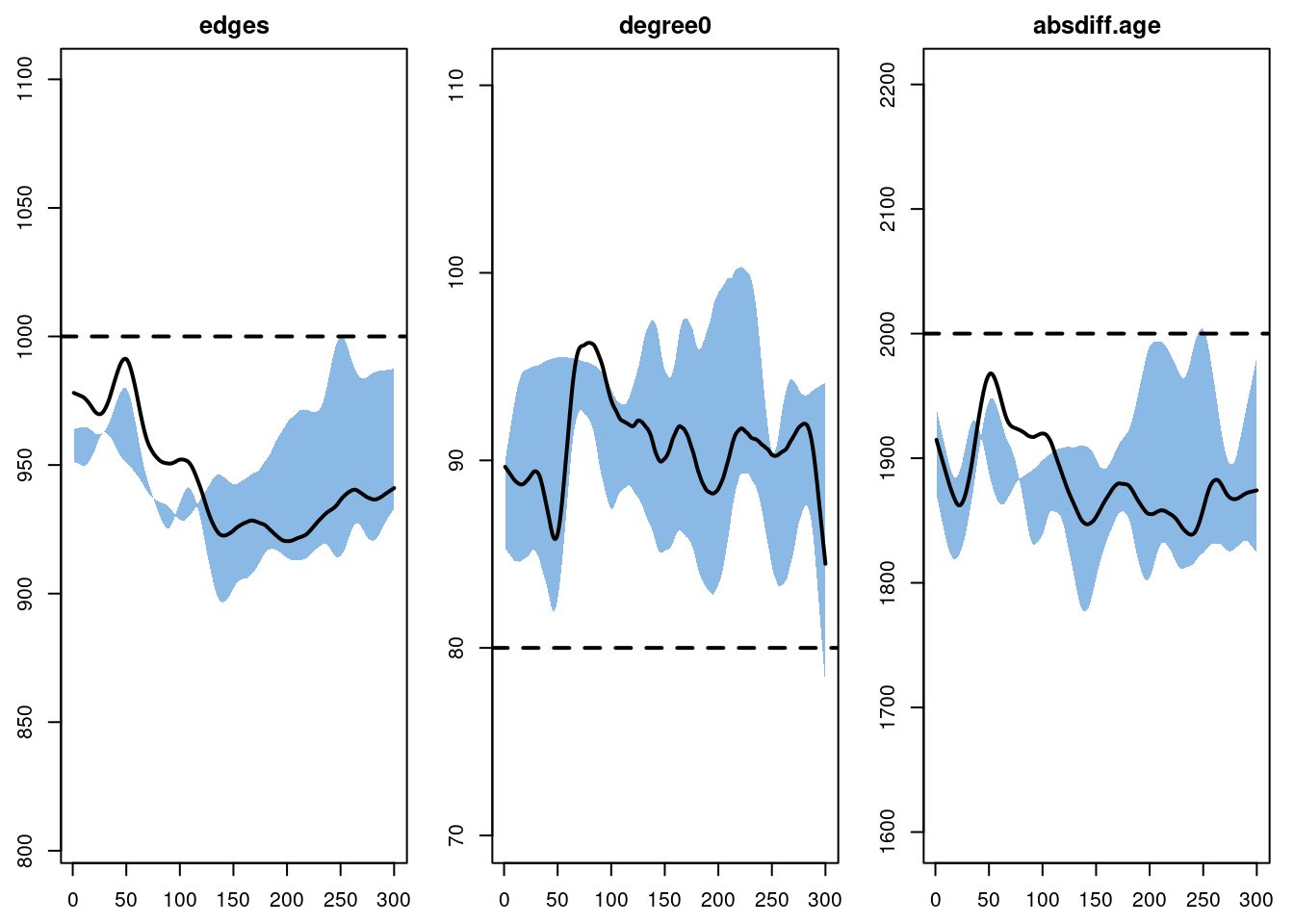
However, it is important to note that the change in edges may be related to underlying reductions in the population size (as a function of relatively high COVID-related mortality). To demonstrate this, we examine the meandeg statistics, which is the per capita mean degree (i.e., it does not depend on the fluctuations in population size). Here, the target statistic is relatively stable (perhaps a minor bias but nothing that will influence the epi outcomes too much).
plot(sim, type = "formation", stats = "meandeg", qnts = 1, ylim = c(1, 3))
abline(h = 2, lty = 2, lwd = 2)
39.7 Epidemic Model Analysis
With the epidemic model simulation complete, let’s inspect the network object. We can see a listing of the modules used, and the model output variables available for inspection. Because we used tergmLite, we only have the summary statistic data and not the individual-level network data.
simEpiModel Simulation
=======================
Model class: netsim
Simulation Summary
-----------------------
Model type:
No. simulations: 5
No. time steps: 300
No. NW groups: 1
Fixed Parameters
---------------------------
inf.prob = 0.1
act.rate = 3
departure.rates = 1.612192e-05 6.794521e-07 6.794521e-07 6.794521e-07
6.794521e-07 3.205479e-07 3.205479e-07 3.205479e-07 3.205479e-07 3.205479e-07
...
departure.disease.mult = 100
arrival.rate = 3.223207e-05
ei.rate = 0.05
ir.rate = 0.05
groups = 1
Model Functions
-----------------------
initialize.FUN
resim_nets.FUN
infection.FUN
departures.FUN
arrivals.FUN
nwupdate.FUN
prevalence.FUN
verbose.FUN
progress.FUN
aging.FUN
Model Output
-----------------------
Variables: s.num i.num num ei.flow ir.flow e.num r.num
meanAge se.flow total.deaths covid.deaths a.flow
Transmissions: sim1 ... sim5
Formation Statistics
-----------------------
Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
edges 1000 944.186 -5.581 5.256 -10.618 12.294 33.191
meandeg NA 1.939 NA 0.005 NA 0.020 0.054
degree0 80 90.870 13.588 0.712 15.270 1.547 9.435
degree1 NA 320.307 NA 1.576 NA 2.779 16.432
degree2 NA 283.207 NA 1.094 NA 4.364 15.258
absdiff.age 2000 1883.049 -5.848 10.984 -10.648 34.166 83.748
Duration and Dissolution Statistics
-----------------------
Not available when:
- `control$tergmLite == TRUE`
- `control$save.network == FALSE`
- `control$save.diss.stats == FALSE`
- dissolution formula is not `~ offset(edges)`
- `keep.diss.stats == FALSE` (if merging)Here is a default plot of all the compartment sizes (all variables ending in .num), with the full quantile range set to 1.
plot(sim, qnts = 1)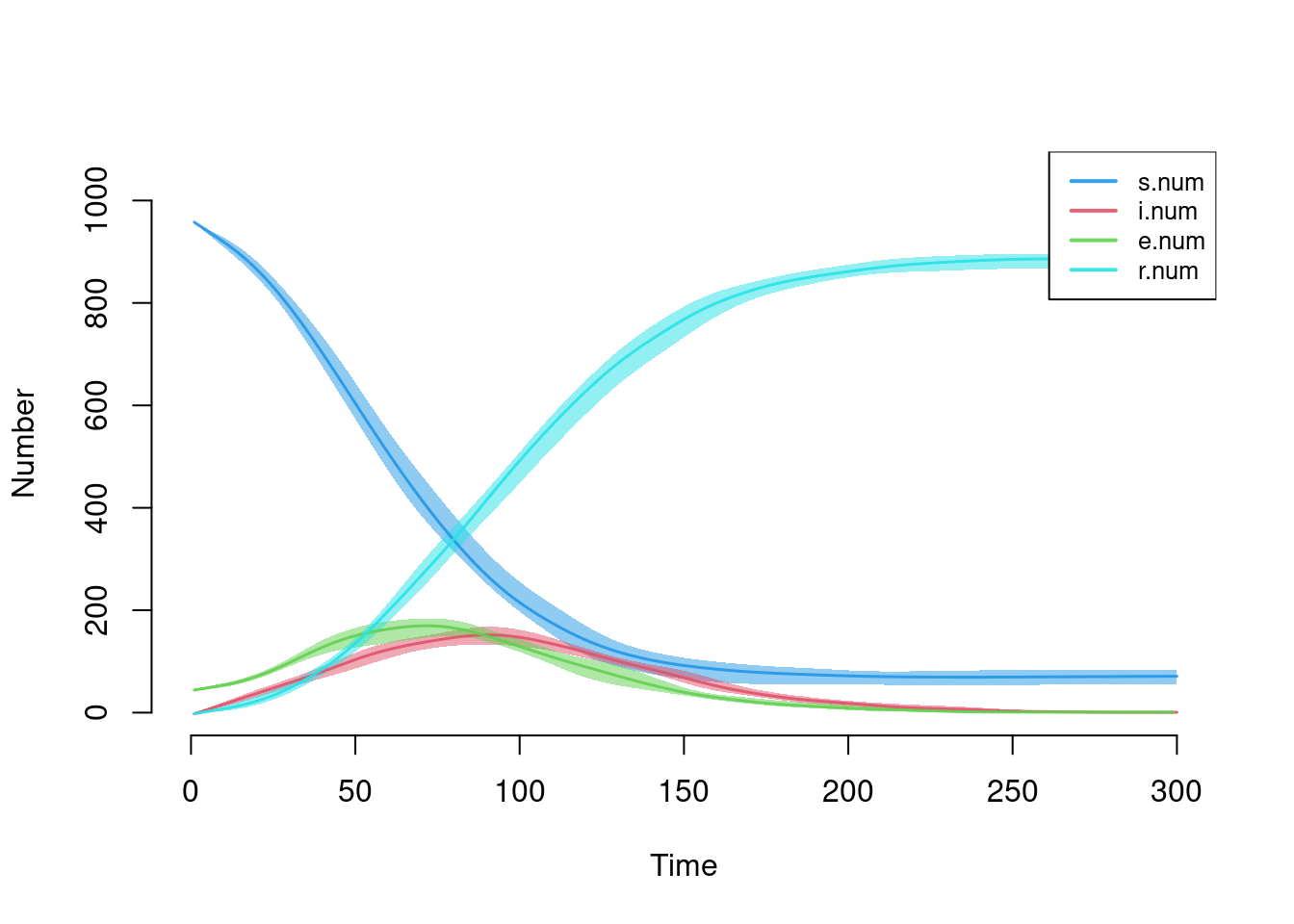
Here is the disease incidence, plotted in two ways:
par(mfrow = c(1,2))
plot(sim, y = "se.flow")
plot(sim, y = "se.flow", mean.smooth = FALSE, qnts = FALSE)
Here is the new mean age summary statistic.
par(mfrow = c(1,1))
plot(sim, y = "meanAge")
Let’s export the data into a data frame that averaged across the simulations and look at the starting and ending numerical values for mean age:
df <- as.data.frame(sim, out = "mean")
head(df$meanAge)[1] NaN 42.12974 42.13248 42.13522 42.12978 42.13252tail(df$meanAge)[1] 40.97602 40.97018 40.97292 40.97566 40.97840 40.98114Here is the decline in the overall population size over time:
plot(sim, y = "num")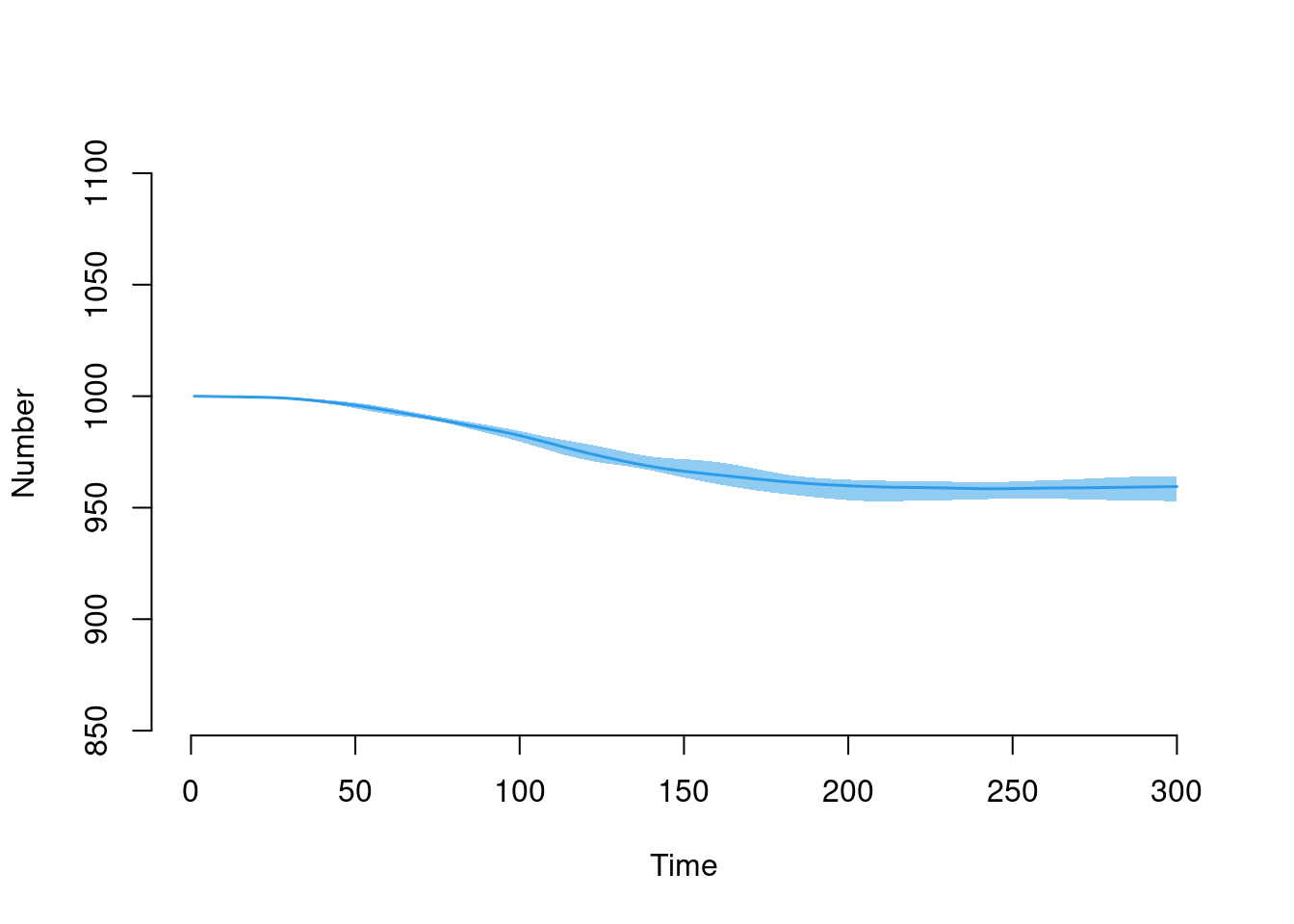
This plot shows the number of new total and COVID-related deaths each day.
plot(sim, y = c("total.deaths", "covid.deaths"), qnts = FALSE, legend = TRUE)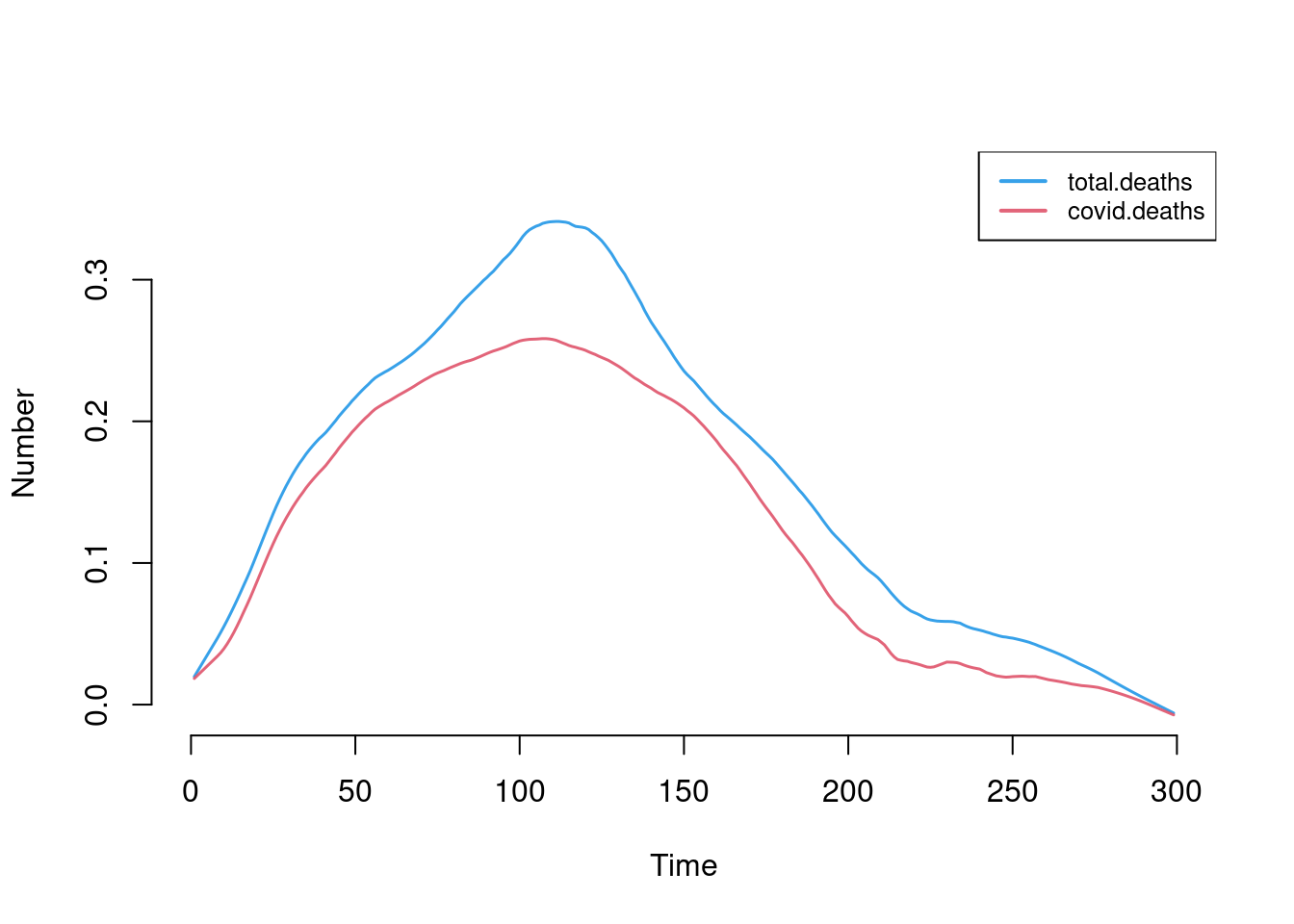
To demonstrate the transmission tree output for this extension model, we can extract the transmission matrix and then plot a phylogram:
tm1 <- get_transmat(sim)
head(tm1, 20)# A tibble: 20 × 6
# Groups: at, sus [20]
at sus inf transProb actRate finalProb
<dbl> <int> <int> <dbl> <dbl> <dbl>
1 3 145 177 0.1 3 0.271
2 3 361 677 0.1 3 0.271
3 3 410 677 0.1 3 0.271
4 3 884 677 0.1 3 0.271
5 4 199 769 0.1 3 0.271
6 4 213 677 0.1 3 0.271
7 4 344 177 0.1 3 0.271
8 4 502 489 0.1 3 0.271
9 4 753 320 0.1 3 0.271
10 4 963 566 0.1 3 0.271
11 4 964 88 0.1 3 0.271
12 5 44 531 0.1 3 0.271
13 5 210 177 0.1 3 0.271
14 5 316 566 0.1 3 0.271
15 5 462 531 0.1 3 0.271
16 5 794 88 0.1 3 0.271
17 6 48 963 0.1 3 0.271
18 6 459 769 0.1 3 0.271
19 6 974 88 0.1 3 0.271
20 7 97 213 0.1 3 0.271# Plot the phylogram for the first seed
phylo.tm1 <- as.phylo.transmat(tm1)found multiple trees, returning a list of 41phylo objectsplot(phylo.tm1[[1]], show.node.label = TRUE, root.edge = TRUE, cex = 0.75)
Overall, it appears that our new demographic features of the model are performing well!