library(EpiModel)23 Working with Nodal Attributes in Network Models
This tutorial will show how to estimate a dynamic network model for a two-group network: instead of one large group of homogeneous nodes, now we’ll have two groups that can differ based on their behavior or biology. Here, we will motivate this with a heterosexual network in which the groups may represent females and males in the population.
To get started, load the EpiModel library.
We also recommend that you clear your environment to avoid any leftover objects from the last tutorials or labs.
rm(list = ls())For this particular tutorial, we will set the seed to ensure reproducible results.
set.seed(12345)23.1 Network Model
For the network model parameterization, we will review how to fit a two-group model with a differential degree distribution by group.
23.1.1 Initialization
The number in each group will be 250 nodes.
num.g1 <- num.g2 <- 250
nw <- network_initialize(n = num.g1 + num.g2)
nw Network attributes:
vertices = 500
directed = FALSE
hyper = FALSE
loops = FALSE
multiple = FALSE
bipartite = FALSE
total edges= 0
missing edges= 0
non-missing edges= 0
Vertex attribute names:
vertex.names
No edge attributesWe use the following function to define a nodal attribute, group, and then set it on the network. We can print out the network again to see that it has been added to the list of vertex attributes. To use group as a special attribute (see paragraph below), the values of group must be 1 and 2 only.
group <- rep(1:2, times = c(num.g1, num.g2))
nw <- set_vertex_attribute(nw, attrname = "group", value = group)
nw Network attributes:
vertices = 500
directed = FALSE
hyper = FALSE
loops = FALSE
multiple = FALSE
bipartite = FALSE
total edges= 0
missing edges= 0
non-missing edges= 0
Vertex attribute names:
group vertex.names
No edge attributesWe can use get_vertex_attribute to extract the same attribute from the network object:
get_vertex_attribute(nw, "group") [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[38] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[75] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[112] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[149] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[186] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
[223] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2
[260] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
[297] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
[334] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
[371] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
[408] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
[445] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
[482] 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2In core EpiModel, the group attribute has a special role for these built-in models that we are exploring in this course. We can, and will, use other nodal attributes on the network to model elements like age or race within the network structure. But group is special because it allows for easy parameterization of heterogeneous epidemic parameters (e.g., group-specific recovery rates). Epidemic parameters stratified by other attributes can also be arbitrarily added, but this requires some additional programming of the epidemic modules in EpiModel. We’ll get to that at the end of Day 4 and spend most of Day 5 on this.
23.1.2 Degree Distributions
Next, the group-specific degree distributions are specified as the fractions of each group that have 0, 1, 2, and 3 or more edges at any one time (momentary degree). Within this two-group framework, the first group will represent women and the second men. In our hypothetical empirical data, women exhibit less concurrency than men, but also fewer isolates. The following are those fractional distributions.
deg.dist.g1 <- c(0.40, 0.55, 0.04, 0.01)
deg.dist.g2 <- c(0.54, 0.31, 0.10, 0.05)In our model, we will use a mean degree of 0.66. How do our degree distributions compare to the distribution expected under a Poisson probability mass function with a rate equal to this the mean degree? The dpois function in R returns the probability mass for degree 0 through 2 and ppois sums the cumulative mass for degree 3+.
pois.dists <- c(dpois(0:2, lambda = 0.66),
ppois(2, lambda = 0.66, lower.tail = FALSE))This barplot compares the two observed and the one estimated fractional degree distribution, each adding to 100%. The degree distribution for men more closely matches that of the Poisson distribution, but still has slightly less concurrency than expected.
par(mar = c(3,3,2,1), mgp = c(2,1,0), mfrow = c(1,1))
barplot(cbind(deg.dist.g1, deg.dist.g2, pois.dists),
beside = TRUE, ylim = c(0, 0.6), col = 1:4)
legend("topright", legend = paste0("deg", 0:3),
pch = 15, col = 1:4,
cex = 0.9, bg = "white")
In this model, we will represent a multi-group network in which there is purely disortative mixing (by sex) to represent heterosexual contact. With this parameterization, and either a differential group size or degree distribution, the overall number of edges expected from each group must match. The EpiModel function check_degdist_bal takes as input two group sizes and two fractional degree distributions and checks whether the total number of implied edges is the same. Note that this constraint of matching edges is relaxed when mixing is not purely disortative (because some edges occur within group); nonetheless, TERGM parameterization still does require a single edges statistic.
check_degdist_bal(num.g1, num.g2,
deg.dist.g1, deg.dist.g2)Degree Distribution Check
=============================================
g1.dist g1.cnt g2.dist g2.cnt
Deg0 0.40 100.0 0.54 135.0
Deg1 0.55 137.5 0.31 77.5
Deg2 0.04 10.0 0.10 25.0
Deg3 0.01 2.5 0.05 12.5
Edges 1.00 165.0 1.00 165.0
=============================================
** Edges balanced ** 23.1.3 Formation and Dissolution
Since we have not specified any nodal attributes for the network other than group, the formation model will only consider aspects of the group-specific degree distribution and mixing on group. ERGM model term degree allows for stratification by a nodal attribute. The 0:1 notation within a single degree term below is a short-hand way of writing multiple degree terms (e.g., degree(0) + degree(1)). The nodematch term is a may to represent the edges on a diagonal of a mixing matrix for the specified attribute (i.e., within group mixing).
formation <- ~edges + degree(0:1, by = "group") + nodematch("group")For the target statistics, we specify the number of edges as a function of mean degree as 0.66 (500/2 * 0.66 = 165). Or we can input the numbers directly from the check_degdist_bal output, where the Edges indicates the edges and the g1.cnt the numbers of group 1 nodes with degree 0 to 3, and g2.cnt the same for group 2 nodes. There are four target statistics needed for the degree terms: 2 for each degree term times 2 for each group. They are input by group and then by degree (so degree 0 for group 1, then degree 1 for group 1, then degree 0 for group 2, and degree 1 for group 2). In this particular model, we will not overfit by including all possible degree terms (i.e., a count of persons with degrees 2 and 3). Finally, the target statistic for nodematch with a purely disortative mixing model is 0: there are no edges between persons matched on the value of the group variable.
target.stats <- c(165, 100, 137.5, 135, 77.5, 0)To recap the formulation of the target statistics:
edgesis a count of edgesdegreeis a count of nodes (whith a particular degree)nodematchis a count of edges (matched on a nodal attribute)
The dissolution model is parameterized the same as the prior example but with a shorter partnership duration than the first tutorial.
coef.diss <- dissolution_coefs(dissolution = ~offset(edges), duration = 10)
coef.dissDissolution Coefficients
=======================
Dissolution Model: ~offset(edges)
Target Statistics: 10
Crude Coefficient: 2.197225
Mortality/Exit Rate: 0
Adjusted Coefficient: 2.19722523.1.4 Estimation
The netest function is used for network model fitting.
est <- netest(nw, formation, target.stats, coef.diss)Warning: 'glpk' selected as the solver, but package 'Rglpk' is not available;
falling back to 'lpSolveAPI'. This should be fine unless the sample size and/or
the number of parameters is very big.For the dynamic diagnostics, we simulate from the model fit. The edges have a small bias, due to the relatively short duration. It is important to consider both the relative and absolute magnitude of the bias here. For our purposes, this fit is good enough to move forward!
dx <- netdx(est, nsims = 10, nsteps = 500, ncores = 5,
nwstats.formula = ~edges + degree(0:3, by = "group"))
Network Diagnostics
-----------------------
- Simulating 10 networks
- Calculating formation statisticsdxEpiModel Network Diagnostics
=======================
Diagnostic Method: Dynamic
Simulations: 10
Time Steps per Sim: 500
Formation Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
edges 165.0 158.975 -3.651 0.478 -12.601 0.748 9.995
deg0.group1 100.0 106.592 6.592 0.316 20.876 0.518 8.014
deg1.group1 137.5 130.463 -5.118 0.309 -22.774 0.636 7.890
deg2.group1 NA 10.656 NA 0.122 NA 0.261 3.114
deg3.group1 NA 1.986 NA 0.045 NA 0.184 1.361
deg0.group2 135.0 138.446 2.553 0.297 11.596 0.618 6.554
deg1.group2 77.5 75.847 -2.133 0.265 -6.242 0.863 6.984
deg2.group2 NA 26.261 NA 0.144 NA 0.397 4.435
deg3.group2 NA 7.525 NA 0.077 NA 0.224 2.501
Duration Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
edges 10 9.966 -0.335 0.047 -0.716 0.129 0.78
Dissolution Diagnostics
-----------------------
Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
edges 0.1 0.1 0.42 0 1.216 0.001 0.024This is confirmed when we plot the diagnostics.
plot(dx)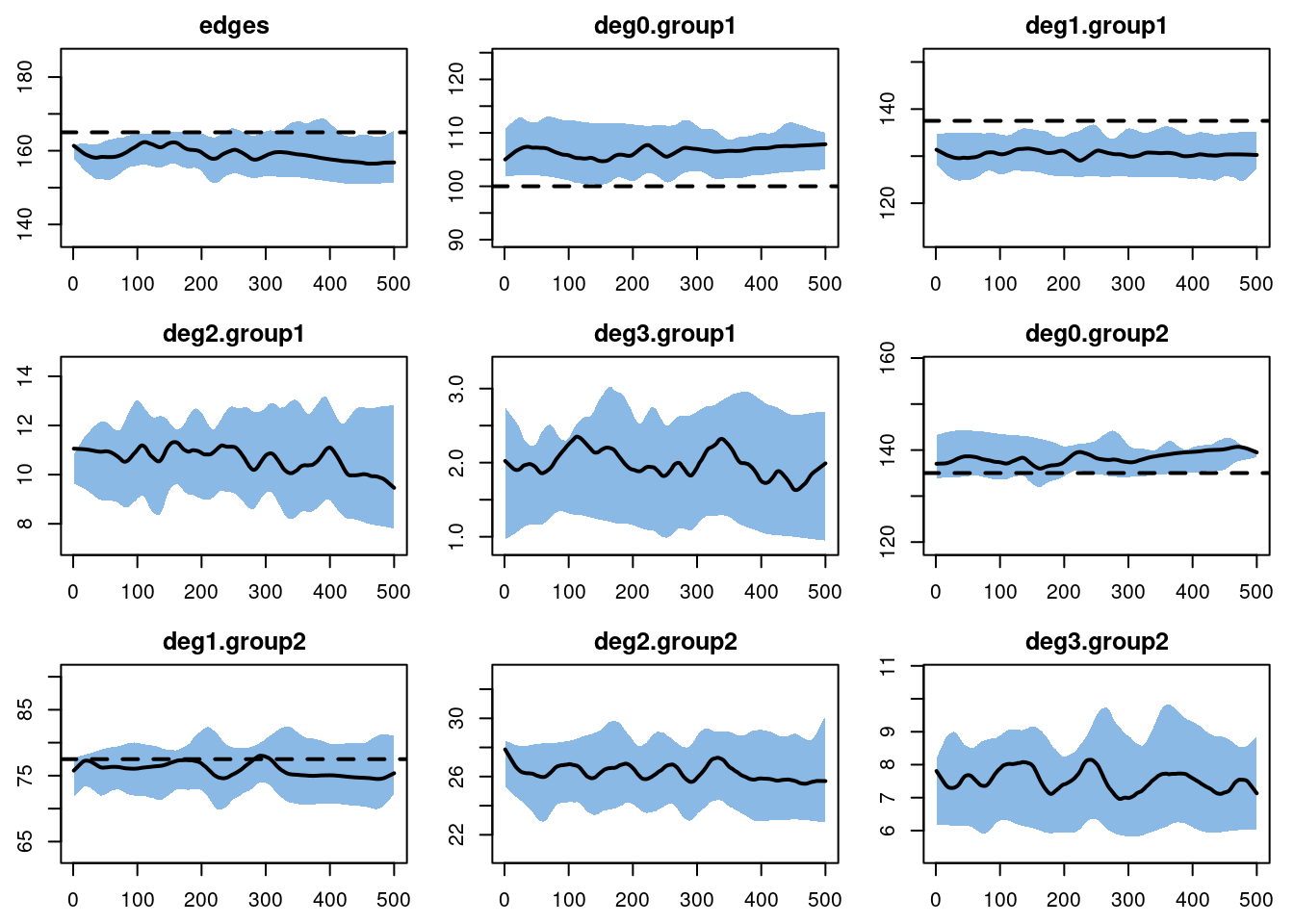
To compare simulations against out-of-model predictions, let’s look again at the expected degree 2 and degree 3 for each group. The simulation means are pretty close to those expectations.
check_degdist_bal(num.g1, num.g2,
deg.dist.g1, deg.dist.g2)Degree Distribution Check
=============================================
g1.dist g1.cnt g2.dist g2.cnt
Deg0 0.40 100.0 0.54 135.0
Deg1 0.55 137.5 0.31 77.5
Deg2 0.04 10.0 0.10 25.0
Deg3 0.01 2.5 0.05 12.5
Edges 1.00 165.0 1.00 165.0
=============================================
** Edges balanced ** 23.2 Epidemic Model
For the disease simulation, we will simulate an SIR epidemic in a closed population.
23.2.1 Parameterization
The epidemic model parameters are below. In this tutorial, we will use biological parameters for the infection probability per act and recovery rates as equal to demonstrate the impact of group-specific degree distributions on outcomes. Note that the group-specific parameters for the infection probability govern the risk of infection to persons in that mode given contact with persons in the other group.
param <- param.net(inf.prob = 0.2, inf.prob.g2 = 0.2,
rec.rate = 0.02, rec.rate.g2 = 0.02)At the outset, 10 people in each group will be infected. For an SIR epidemic simulation, it is necessary to specify the number recovered in each group, here starting at 0.
init <- init.net(i.num = 10, i.num.g2 = 10,
r.num = 0, r.num.g2 = 0)For control settings, we will simulate 5 epidemics over 500 time steps each. Here we use the multi-core functionality in our controls.
control <- control.net(type = "SIR", nsims = 5, nsteps = 500, ncores = 5)23.2.2 Simulation
The model is simulated by inputting the fitted network model, the epidemic parameters, the initial conditions, and control settings.
sim <- netsim(est, param, init, control)Printing the model object shows the inputs and outputs from the simulation object. In particular, take note of the Variables listing; the epidemic outputs for Group 1 are listed without a suffix whereas the outputs for Group 2 are listed with a .g2 suffix.
simEpiModel Simulation
=======================
Model class: netsim
Simulation Summary
-----------------------
Model type: SIR
No. simulations: 5
No. time steps: 500
No. NW groups: 2
Fixed Parameters
---------------------------
inf.prob = 0.2
rec.rate = 0.02
inf.prob.g2 = 0.2
rec.rate.g2 = 0.02
act.rate = 1
groups = 2
Model Output
-----------------------
Variables: s.num i.num r.num num s.num.g2 i.num.g2
r.num.g2 num.g2 si.flow si.flow.g2 ir.flow ir.flow.g2
Networks: sim1 ... sim5
Transmissions: sim1 ... sim5
Formation Statistics
-----------------------
Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means)
edges 165.0 158.024 -4.228 0.626 -11.134 1.087
deg0.group1 100.0 107.013 7.013 0.441 15.909 0.591
deg1.group1 137.5 130.476 -5.108 0.398 -17.629 0.327
deg0.group2 135.0 138.878 2.873 0.418 9.269 0.666
deg1.group2 77.5 75.554 -2.511 0.432 -4.509 1.048
nodematch.group 0.0 0.000 NaN NaN NaN 0.000
SD(Statistic)
edges 9.649
deg0.group1 7.783
deg1.group1 7.746
deg0.group2 6.533
deg1.group2 7.476
nodematch.group 0.000
Duration Statistics
-----------------------
Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
edges 10 10.03 0.303 0.064 0.471 0.138 0.772
Dissolution Statistics
-----------------------
Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
edges 0.1 0.1 -0.005 0 -0.012 0.001 0.024Note also that the print output includes the names of the individual modules. For these two-group models, EpiModel automatically selects which modules and functions to use. For extension modules (that do not have have a type input), you will need to specify this.
23.2.3 Analysis
Similar to the first tutorial, plotting the netsim object shows the prevalence for each disease state in the model over time.
par(mfrow = c(1, 1))
plot(sim, main = "Disease State Sizes")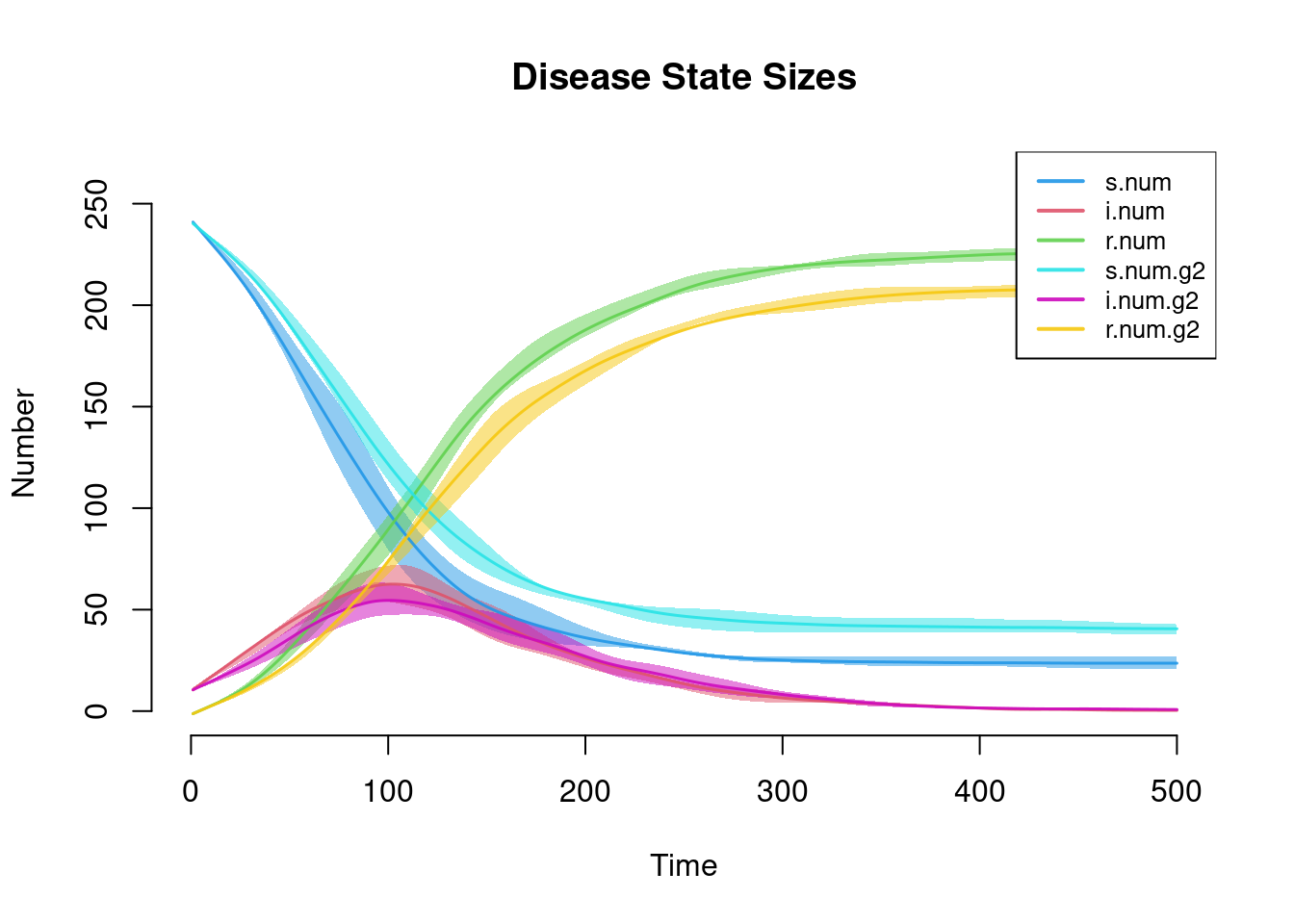
This plot more clearly shows prevalence and incidence by mode. Interestingly, women (Group 1) have a slightly higher prevalence of disease during the main epidemic period, and more women than men end up in the recovered state. Men and women have the same mean degree but men have a higher prevalence of concurrency (degree 2+) than women. Following epidemiological and network theory, conditional on mean degree (which is the same for both groups in this model), concurrency increases the risk of transmission but not acquisition. So therefore, women bear the higher burden of male concurrency. Your course instructor, Steve Goodreau, has prepared an excellent tutorial and exercise set on this topic.
par(mfrow = c(1,2))
plot(sim, y = c("i.num", "i.num.g2"), popfrac = TRUE,
qnts = FALSE, ylim = c(0, 0.4), legend = TRUE)
plot(sim, y = c("si.flow", "si.flow.g2"),
qnts = FALSE, ylim = c(0, 2.5), legend = TRUE)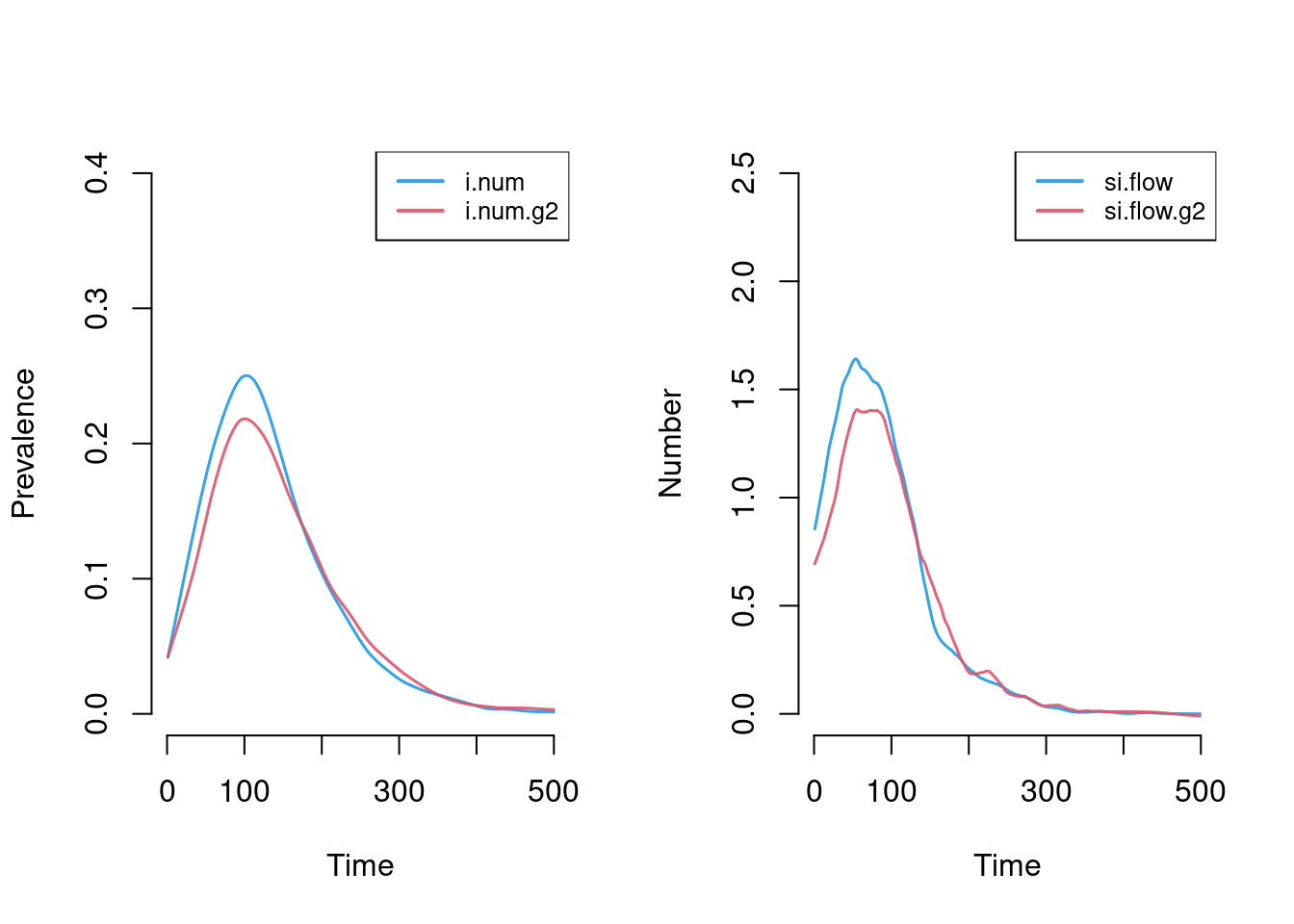
It is possible to plot the color-coded static network at various time points during the simulation, as in the last tutorial. This helps to visualize how womens’ (circle) risk is dependent on their male (square) partners’ network connections.
par(mfrow = c(1, 1), mar = c(0, 0, 0, 0))
plot(sim, type = "network", col.status = TRUE, at = 50,
sims = "mean", shp.g2 = "square")
It is possible to add new variables to an existing model object with mutate_epi, which takes inspiration from the mutate functions in the tidyverse. With a time step unit of a week, we can calculate standardized incidence rates per 100 person-years at risk using the following approach. The mutate_epi function takes a netsim object and adds a new variable.
sim <- mutate_epi(sim, ir.g1 = (si.flow / s.num) * 100 * 52,
ir.g2 = (si.flow.g2 / s.num.g2) * 100 * 52)Printing out the object, you can see that these two new variables are in the variable list.
simEpiModel Simulation
=======================
Model class: netsim
Simulation Summary
-----------------------
Model type: SIR
No. simulations: 5
No. time steps: 500
No. NW groups: 2
Fixed Parameters
---------------------------
inf.prob = 0.2
rec.rate = 0.02
inf.prob.g2 = 0.2
rec.rate.g2 = 0.02
act.rate = 1
groups = 2
Model Output
-----------------------
Variables: s.num i.num r.num num s.num.g2 i.num.g2
r.num.g2 num.g2 si.flow si.flow.g2 ir.flow ir.flow.g2 ir.g1
ir.g2
Networks: sim1 ... sim5
Transmissions: sim1 ... sim5
Formation Statistics
-----------------------
Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means)
edges 165.0 158.024 -4.228 0.626 -11.134 1.087
deg0.group1 100.0 107.013 7.013 0.441 15.909 0.591
deg1.group1 137.5 130.476 -5.108 0.398 -17.629 0.327
deg0.group2 135.0 138.878 2.873 0.418 9.269 0.666
deg1.group2 77.5 75.554 -2.511 0.432 -4.509 1.048
nodematch.group 0.0 0.000 NaN NaN NaN 0.000
SD(Statistic)
edges 9.649
deg0.group1 7.783
deg1.group1 7.746
deg0.group2 6.533
deg1.group2 7.476
nodematch.group 0.000
Duration Statistics
-----------------------
Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
edges 10 10.03 0.303 0.064 0.471 0.138 0.772
Dissolution Statistics
-----------------------
Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
edges 0.1 0.1 -0.005 0 -0.012 0.001 0.024After we add the new variable, we can plot and analyze it like any other built-in variable.
par(mar = c(3,3,2,1))
plot(sim, y = c("ir.g1", "ir.g2"), legend = TRUE,
main = "Standardized Incidence Rates by Group")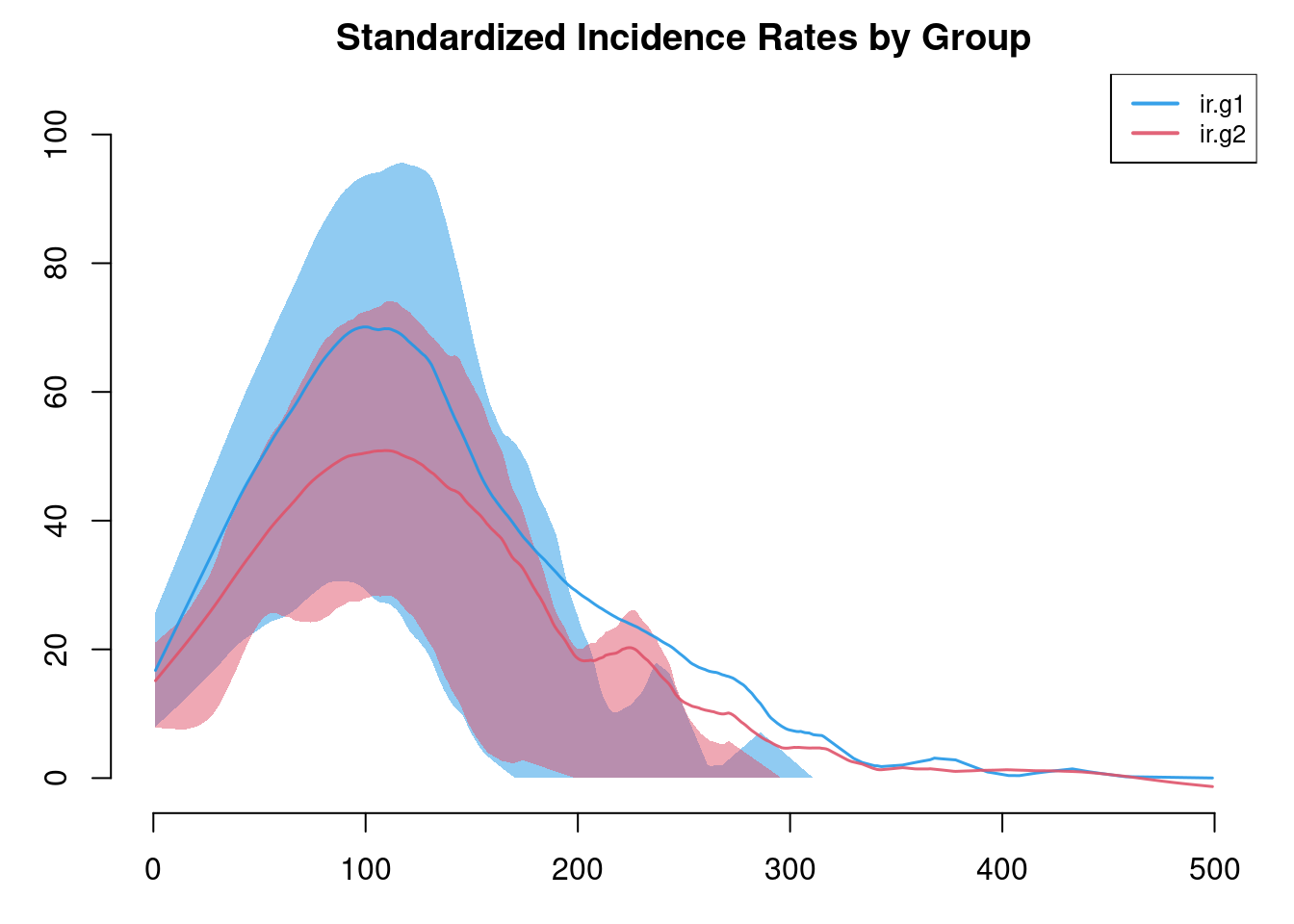
Incidence rates in particular are often highly variable. The plot by default will use a loess smoother so some of this variability may be lost. Therefore, it is worth inspecting the non-smoothed plots too.
plot(sim, y = c("ir.g1", "ir.g2"), legend = TRUE,
mean.smooth = FALSE, qnts = FALSE, mean.lwd = 1,
main = "Standardized Incidence Rates by Group (Non-Smoothed)")
As another exercise, let’s extract the data into a data frame and then calculate some other relevant summary statistics. By default as.data.frame will extract the individual simulation data in each row, but by specifying out = "mean" we can see the time specific averages for all the variables across simulations. The variables in this data frame include both the original variables from netsim plus the two new ones we added with mutate_epi.
df <- as.data.frame(sim, out = "mean")
head(df, 10) time s.num i.num r.num num s.num.g2 i.num.g2 r.num.g2 num.g2 si.flow
1 1 240.0 10.0 0.0 250 240.0 10.0 0.0 250 NaN
2 2 238.6 11.4 0.0 250 238.2 11.8 0.0 250 1.4
3 3 237.0 13.0 0.0 250 237.6 12.2 0.2 250 1.6
4 4 235.8 13.6 0.6 250 236.4 13.4 0.2 250 1.2
5 5 235.2 13.8 1.0 250 236.0 13.6 0.4 250 0.6
6 6 235.0 13.6 1.4 250 235.4 14.0 0.6 250 0.2
7 7 234.2 14.2 1.6 250 234.4 14.4 1.2 250 0.8
8 8 233.2 15.2 1.6 250 234.4 14.0 1.6 250 1.0
9 9 232.6 15.6 1.8 250 234.2 14.0 1.8 250 0.6
10 10 231.0 17.0 2.0 250 234.0 14.2 1.8 250 1.6
si.flow.g2 ir.flow ir.flow.g2 ir.g1 ir.g2
1 NaN NaN NaN NaN NaN
2 1.8 0.0 0.0 30.533385 39.421008
3 0.6 0.0 0.2 35.124235 13.183307
4 1.2 0.6 0.0 26.478341 26.366460
5 0.4 0.4 0.2 13.352571 8.813559
6 0.6 0.4 0.2 4.444444 13.276756
7 1.0 0.2 0.6 17.854406 22.261026
8 0.0 0.0 0.4 22.241786 0.000000
9 0.2 0.2 0.2 13.506998 4.463519
10 0.2 0.2 0.0 36.097817 4.444444One interesting summary statistic for an SIR epidemic is the cumulative incidence. Here are the mean cumulative incidences in the first and second groups across simulations. It is necessary here to use na.rm = TRUE to calculate these statistics by removing the first row where the value is undefined.
sum(df$si.flow, na.rm = TRUE)[1] 216.4sum(df$si.flow.g2, na.rm = TRUE)[1] 199.4Here are two more that may be of interest: the time point of the peak standardized incidence rates, and also the value of the incidence rate at that time point.
which.max(df$ir.g1)[1] 132df$ir.g1[which.max(df$ir.g1)][1] 196.6157plot(sim, y = "ir.g1",
mean.smooth = FALSE, qnts = FALSE, mean.lwd = 1,
main = "Time and Value of Peak Incidence in Females (Group 1)")
points(which.max(df$ir.g1), df$ir.g1[which.max(df$ir.g1)], cex = 3)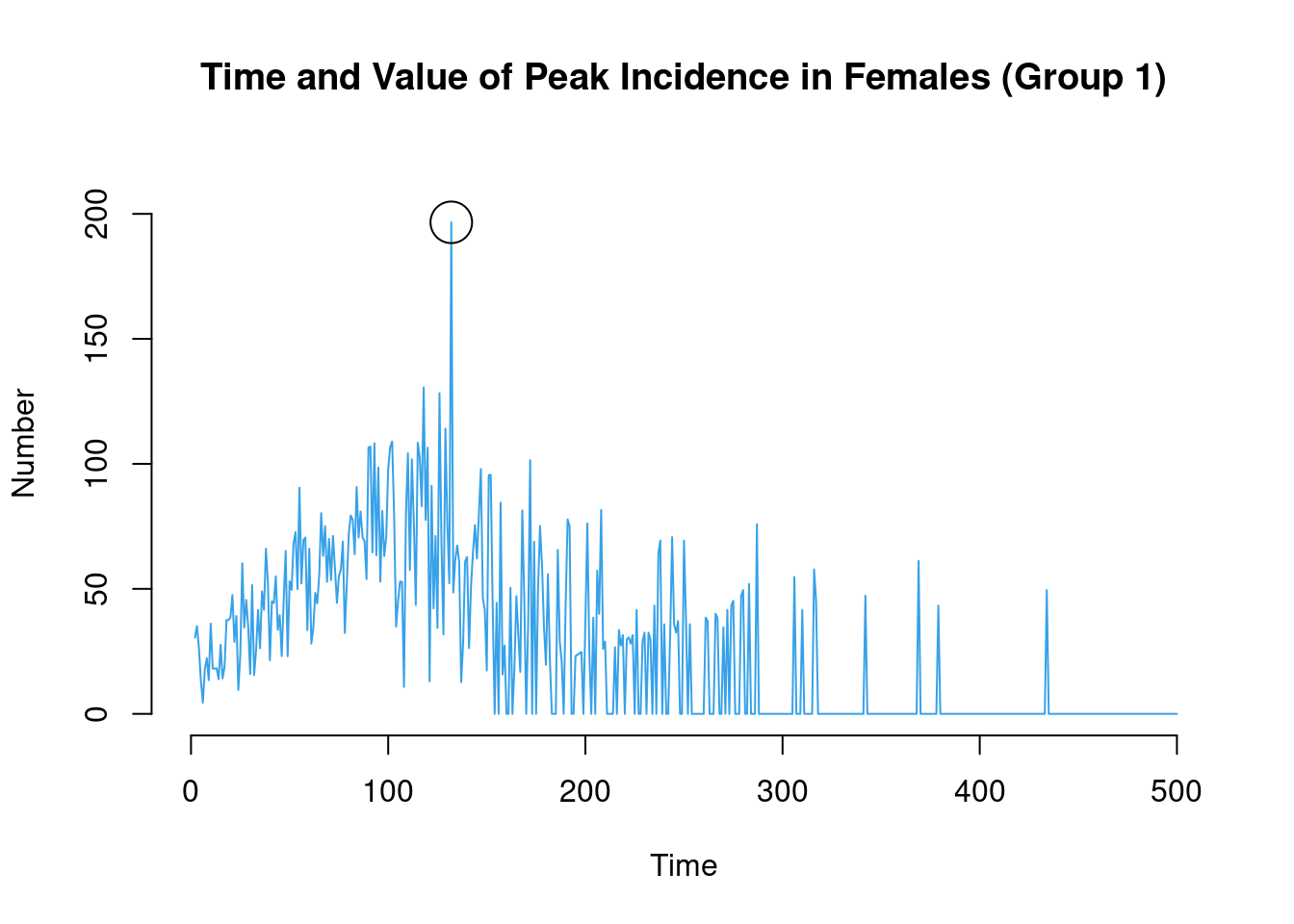
The transmission matrix again shows the individual transmission events that occurred at each time step, along with information about the infecting partner that may be relevant.
tm <- get_transmat(sim)
head(tm, 15)# A tibble: 15 × 7
# Groups: at, sus [15]
at sus inf infDur transProb actRate finalProb
<dbl> <int> <int> <dbl> <dbl> <dbl> <dbl>
1 2 184 367 15 0.2 1 0.2
2 2 222 310 22 0.2 1 0.2
3 2 260 191 28 0.2 1 0.2
4 2 286 65 115 0.2 1 0.2
5 2 322 98 17 0.2 1 0.2
6 2 476 157 55 0.2 1 0.2
7 3 198 389 7 0.2 1 0.2
8 4 201 294 8 0.2 1 0.2
9 7 143 260 5 0.2 1 0.2
10 7 233 286 5 0.2 1 0.2
11 8 156 476 6 0.2 1 0.2
12 10 57 389 14 0.2 1 0.2
13 10 229 260 8 0.2 1 0.2
14 11 489 65 124 0.2 1 0.2
15 12 88 489 1 0.2 1 0.2The infDur column shows the duration of infection (in time steps) of the infecting partner at the point of transmission. For example, an event with an infDur of 1 means that the infecting partner had just become infected themselves in the prior time step. This is the proportion of transmission that occured in that state.
mean(tm$infDur == 1)[1] 0.05651106One can also convert this into a phylogeny for easier visualization of these transmission chains. First, we convert the transmission matrix into a phylo class object that can then be further analyzed and visualized with the ape package. In this transmission matrix, there are multiple trees found because we seeded the infection with 20 people as initial conditions.
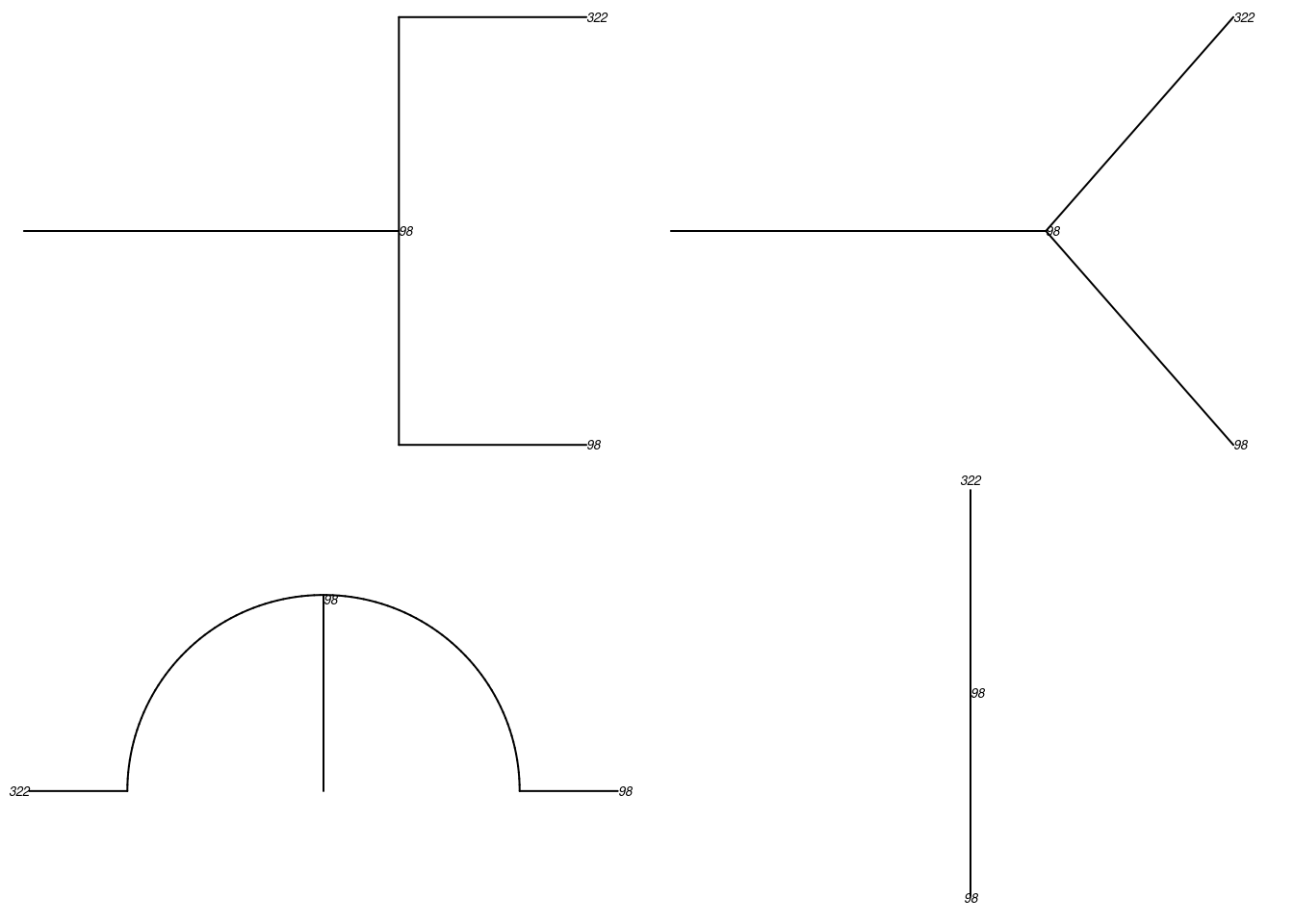
tmPhylo <- as.phylo.transmat(tm)found multiple trees, returning a list of 17phylo objectsHere is a standard phylogram of the first four trees. Some initial seeds lead to many downstream infections whereas others do not. Is this a function of underlying contact networks of the seeded nodes, the biology or behavior of those nodes, or something else? This could all be tested!
par(mfrow = c(2, 2), mar = c(0, 0, 0, 0))
plot(tmPhylo[[1]], show.node.label = TRUE, root.edge = TRUE, cex = 0.5)
plot(tmPhylo[[2]], show.node.label = TRUE, root.edge = TRUE, cex = 0.5)
plot(tmPhylo[[3]], show.node.label = TRUE, root.edge = TRUE, cex = 0.5)
plot(tmPhylo[[4]], show.node.label = TRUE, root.edge = TRUE, cex = 0.5)
In phylo objects with multiple trees, each tree is stored with a named object. Note that these names correspond to the ID numbers in the transmission matrix itself. We can extract one tree like so:
names(tmPhylo) [1] "seed_367" "seed_310" "seed_191" "seed_65" "seed_98" "seed_157"
[7] "seed_389" "seed_294" "seed_121" "seed_483" "seed_38" "seed_465"
[13] "seed_255" "seed_187" "seed_321" "seed_409" "seed_124"tmPhylo5 <- tmPhylo[[5]]Then we can plot that particular tree as a phylogram and other visual types included in the ape package.
par(mfrow = c(2, 2), mar = c(0, 0, 0, 0))
plot(tmPhylo5, type = "phylogram",
show.node.label = TRUE, root.edge = TRUE, cex = 0.5)
plot(tmPhylo5, type = "cladogram",
show.node.label = TRUE, root.edge = TRUE, cex = 0.5)
plot(tmPhylo5, type = "fan",
show.node.label = TRUE, root.edge = TRUE, cex = 0.5)
plot(tmPhylo5, type = "unrooted",
show.node.label = TRUE, root.edge = TRUE, cex = 0.5)