Left-truncates simulation epidemiological summary statistics and network statistics at a specified time step.
Usage
truncate_sim(x, at, reset.time)
# S3 method for class 'dcm'
truncate_sim(x, at, reset.time = TRUE)
# S3 method for class 'icm'
truncate_sim(x, at, reset.time = TRUE)
# S3 method for class 'netsim'
truncate_sim(x, at, reset.time = TRUE)Details
This function would be used when running a follow-up simulation from time
steps b to c after a burn-in period from time a to
b, where the final time window of interest for data analysis is
b to c only.
Examples
# DCM examples
param <- param.dcm(inf.prob = 0.2, act.rate = 0.25)
init <- init.dcm(s.num = 500, i.num = 1)
control <- control.dcm(type = "SI", nsteps = 200)
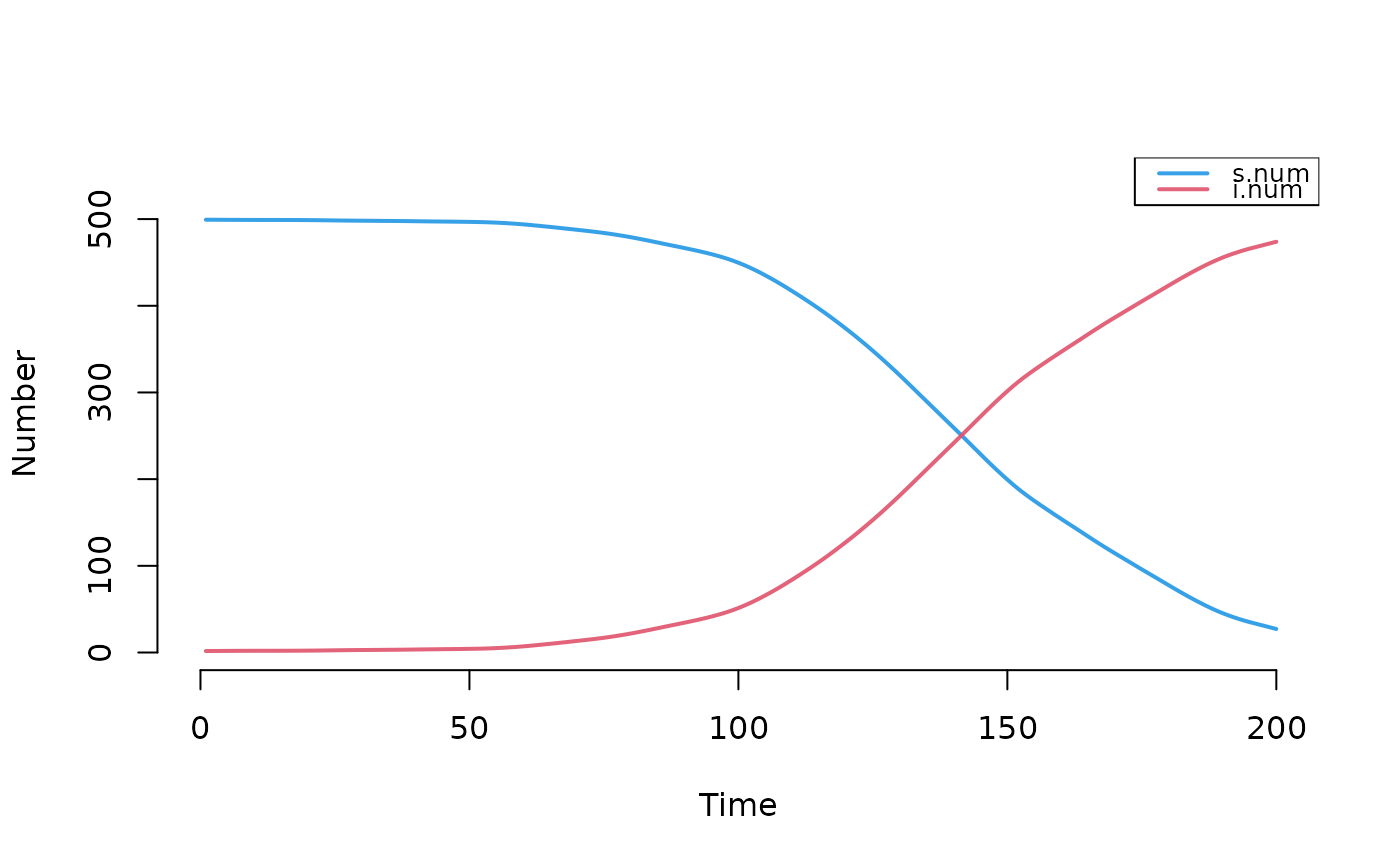
mod1 <- dcm(param, init, control)
plot(mod1)
 # Reset time
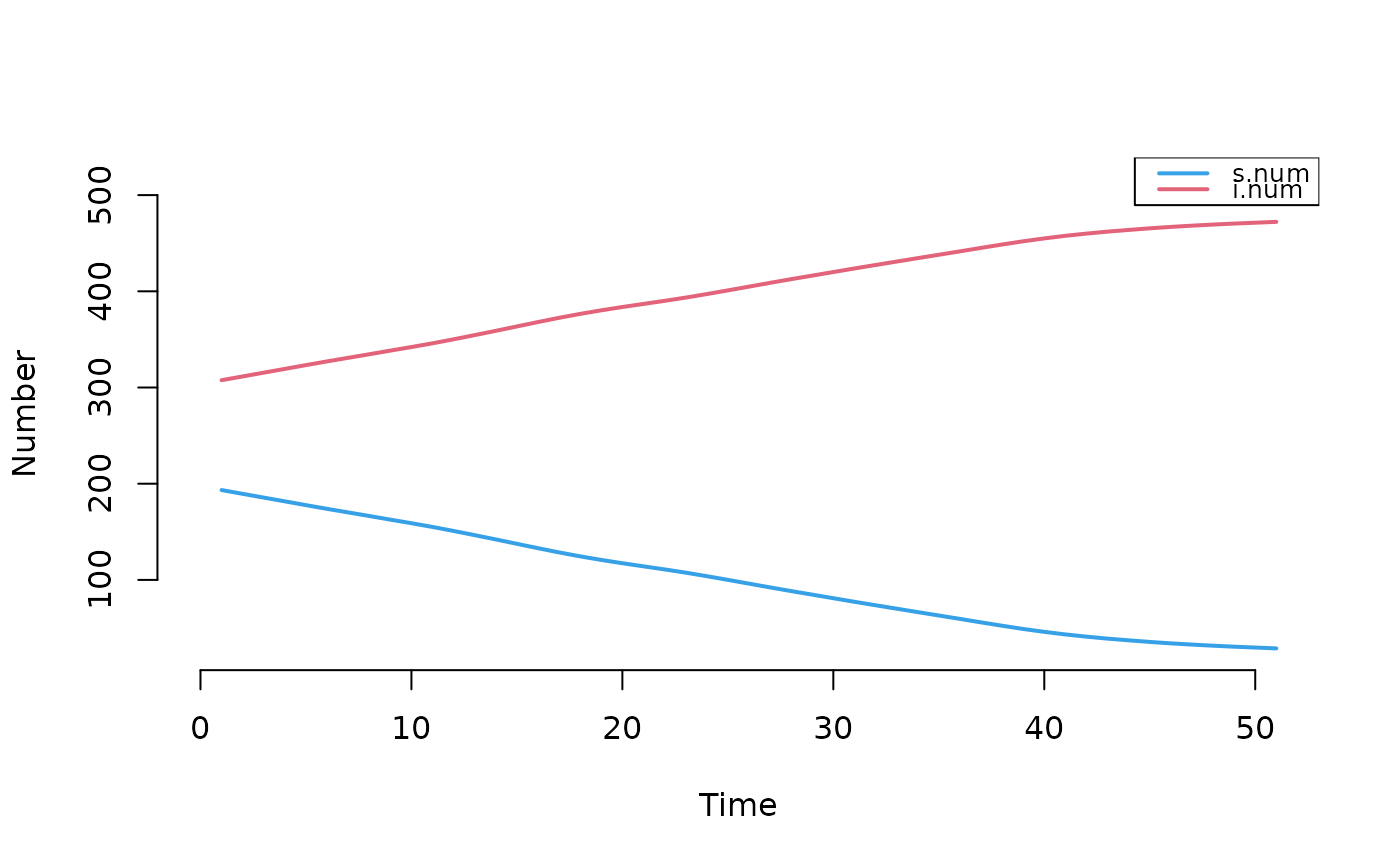
mod2a <- truncate_sim(mod1, at = 150)
plot(mod2a)
# Reset time
mod2a <- truncate_sim(mod1, at = 150)
plot(mod2a)
 head(as.data.frame(mod2a))
#> time s.num i.num si.flow num
#> 1 1 112.84477 388.1552 4.311259 501
#> 2 2 108.53351 392.4665 4.190824 501
#> 3 3 104.34268 396.6573 4.070347 501
#> 4 4 100.27233 400.7277 3.950123 501
#> 5 5 96.32221 404.6778 3.830429 501
#> 6 6 92.49178 408.5082 3.711522 501
# Do not reset time
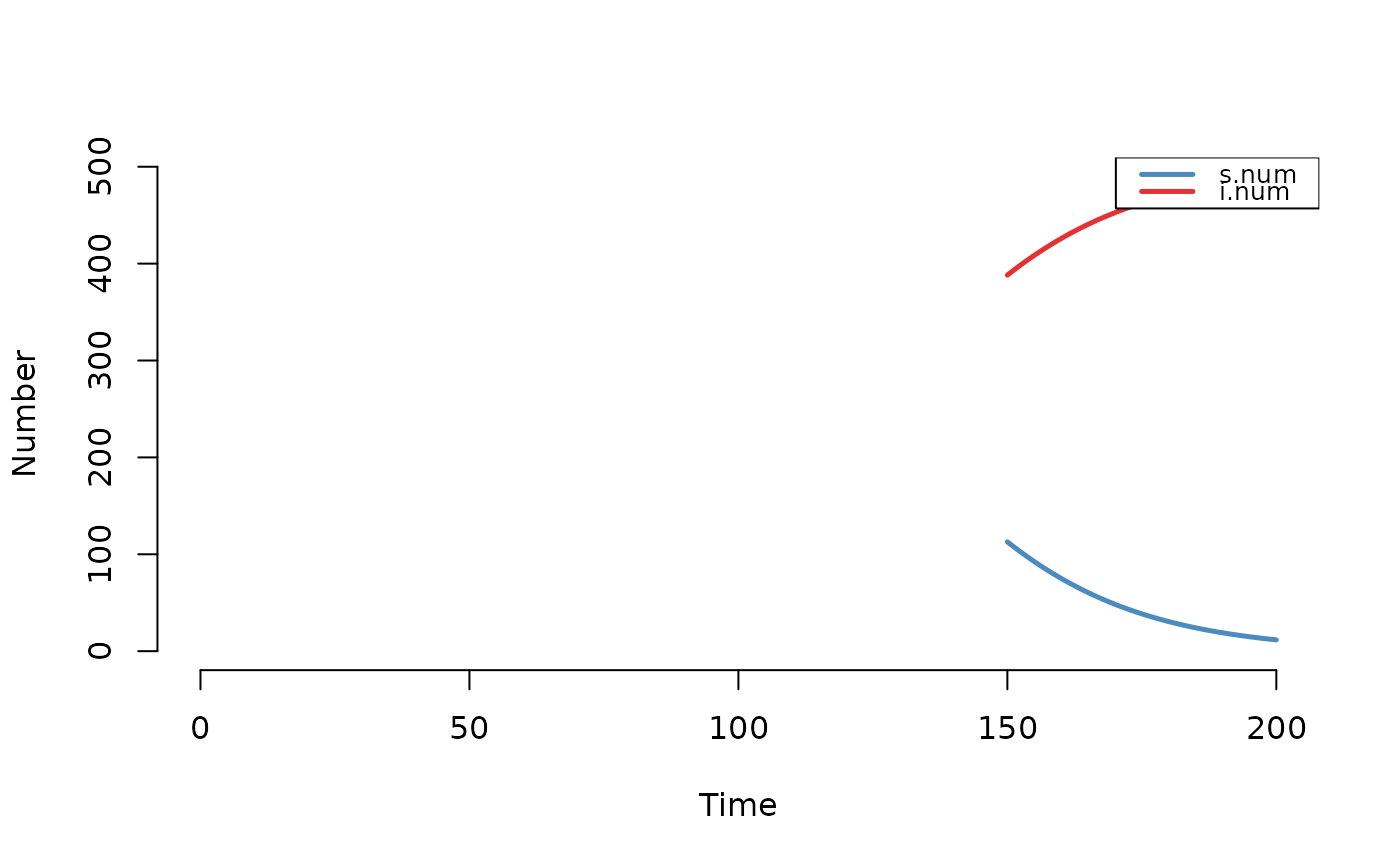
mod2b <- truncate_sim(mod1, at = 150, reset.time = FALSE)
plot(mod2b)
head(as.data.frame(mod2a))
#> time s.num i.num si.flow num
#> 1 1 112.84477 388.1552 4.311259 501
#> 2 2 108.53351 392.4665 4.190824 501
#> 3 3 104.34268 396.6573 4.070347 501
#> 4 4 100.27233 400.7277 3.950123 501
#> 5 5 96.32221 404.6778 3.830429 501
#> 6 6 92.49178 408.5082 3.711522 501
# Do not reset time
mod2b <- truncate_sim(mod1, at = 150, reset.time = FALSE)
plot(mod2b)
 head(as.data.frame(mod2b))
#> time s.num i.num si.flow num
#> 1 150 112.84477 388.1552 4.311259 501
#> 2 151 108.53351 392.4665 4.190824 501
#> 3 152 104.34268 396.6573 4.070347 501
#> 4 153 100.27233 400.7277 3.950123 501
#> 5 154 96.32221 404.6778 3.830429 501
#> 6 155 92.49178 408.5082 3.711522 501
# ICM example
param <- param.icm(inf.prob = 0.2, act.rate = 0.25)
init <- init.icm(s.num = 500, i.num = 1)
control <- control.icm(type = "SI", nsteps = 200, nsims = 1)
mod1 <- icm(param, init, control)
# Reset time
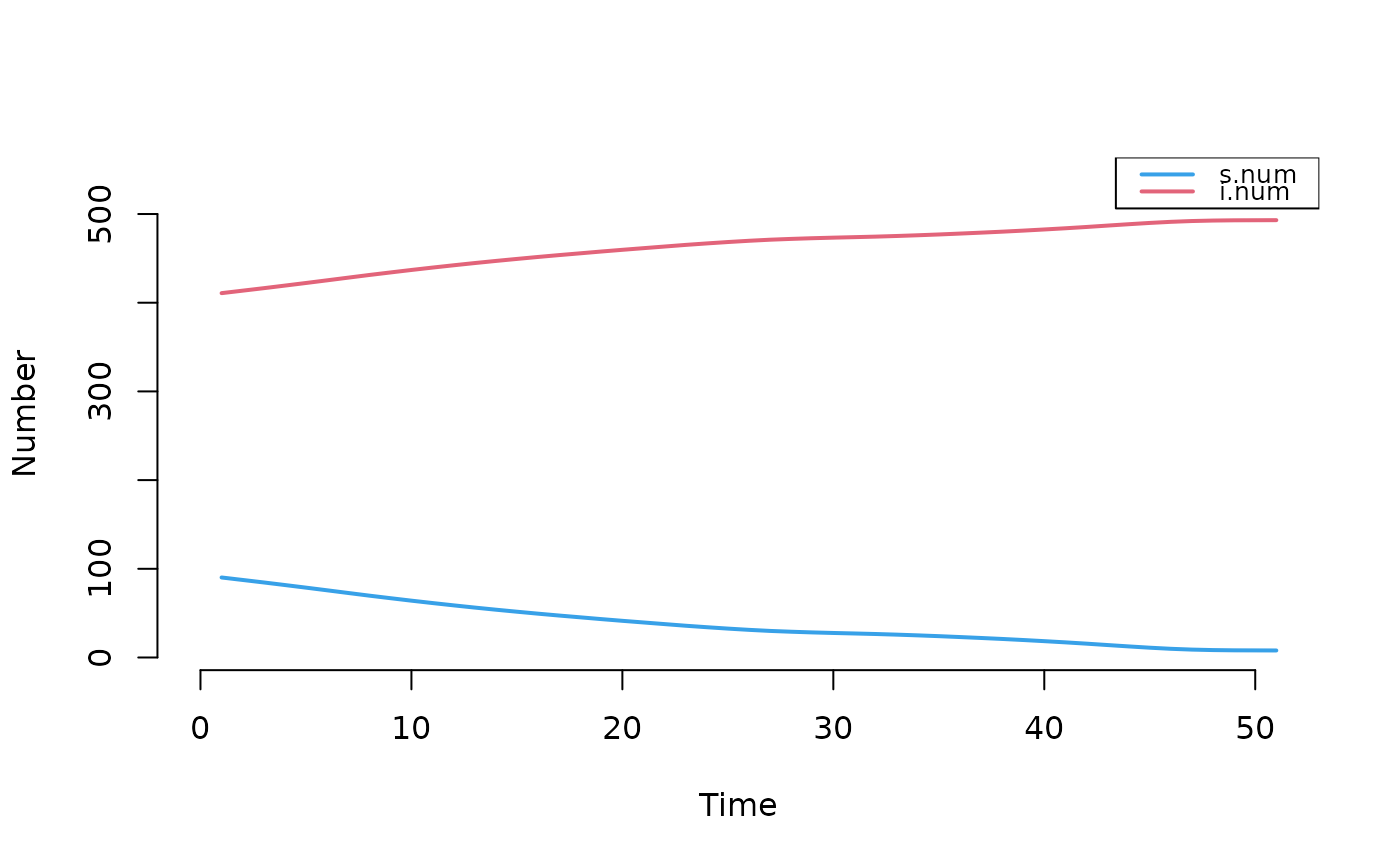
mod2a <- truncate_sim(mod1, at = 150)
plot(mod2a)
head(as.data.frame(mod2b))
#> time s.num i.num si.flow num
#> 1 150 112.84477 388.1552 4.311259 501
#> 2 151 108.53351 392.4665 4.190824 501
#> 3 152 104.34268 396.6573 4.070347 501
#> 4 153 100.27233 400.7277 3.950123 501
#> 5 154 96.32221 404.6778 3.830429 501
#> 6 155 92.49178 408.5082 3.711522 501
# ICM example
param <- param.icm(inf.prob = 0.2, act.rate = 0.25)
init <- init.icm(s.num = 500, i.num = 1)
control <- control.icm(type = "SI", nsteps = 200, nsims = 1)
mod1 <- icm(param, init, control)
# Reset time
mod2a <- truncate_sim(mod1, at = 150)
plot(mod2a)
 head(as.data.frame(mod2a))
#> sim time s.num i.num num si.flow
#> 1 1 1 90 411 501 4
#> 2 1 2 87 414 501 3
#> 3 1 3 85 416 501 2
#> 4 1 4 83 418 501 2
#> 5 1 5 78 423 501 5
#> 6 1 6 77 424 501 1
# Do not reset time
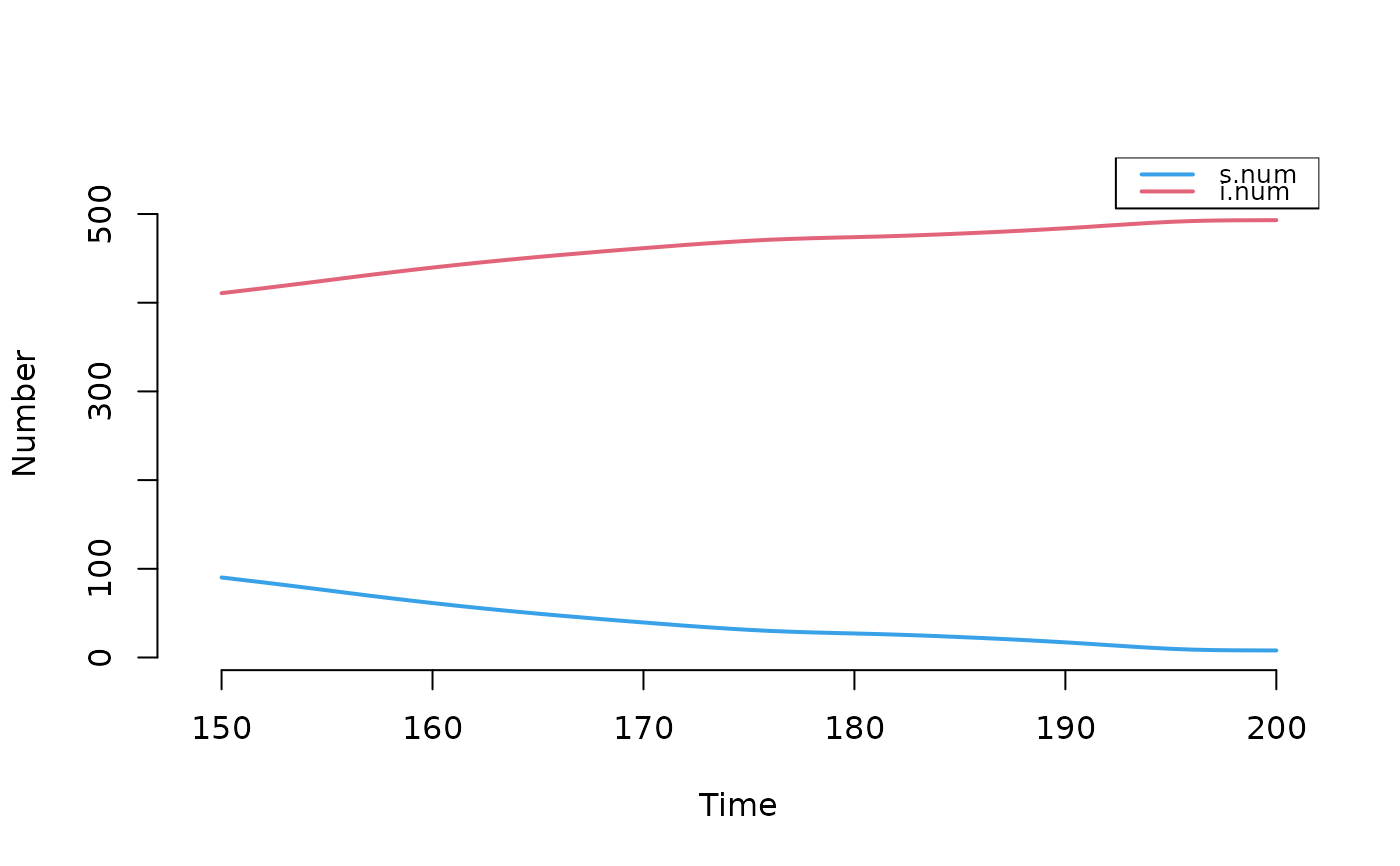
mod2b <- truncate_sim(mod1, at = 150, reset.time = FALSE)
plot(mod2b)
head(as.data.frame(mod2a))
#> sim time s.num i.num num si.flow
#> 1 1 1 90 411 501 4
#> 2 1 2 87 414 501 3
#> 3 1 3 85 416 501 2
#> 4 1 4 83 418 501 2
#> 5 1 5 78 423 501 5
#> 6 1 6 77 424 501 1
# Do not reset time
mod2b <- truncate_sim(mod1, at = 150, reset.time = FALSE)
plot(mod2b)
 head(as.data.frame(mod2b))
#> sim time s.num i.num num si.flow
#> 1 1 150 90 411 501 4
#> 2 1 151 87 414 501 3
#> 3 1 152 85 416 501 2
#> 4 1 153 83 418 501 2
#> 5 1 154 78 423 501 5
#> 6 1 155 77 424 501 1
head(as.data.frame(mod2b))
#> sim time s.num i.num num si.flow
#> 1 1 150 90 411 501 4
#> 2 1 151 87 414 501 3
#> 3 1 152 85 416 501 2
#> 4 1 153 83 418 501 2
#> 5 1 154 78 423 501 5
#> 6 1 155 77 424 501 1