Working with Model Parameters in EpiModel

Introduction

In a model, parameters are the input variables used to define aspects of the system behavior. In the basic built-in SIS (Susceptible-Infected-Susceptible) model, these parameters could be the act rate, the infection probability and the recovery rate. In simple models, each of these parameters are single fixed values that do not change over the course of a simulation. In more complex models, we may want more flexibility in model parameterization.

Therefore, in this vignette, we demonstrate how to implement:

Scenarios: sets of parameters to be changed for a simulation, either at the start or at a specific timestep.
Random parameters: distributions of possible values rather than a single fixed value.
Time-varying parameters and control settings: The scenarios functionality provides the most straightforward way to implement time-varying parameters, but more direct functionality is demonstrated here for advanced users seeking to implement time-varying parameters or control settings.

Scenarios

Scenarios can be defined as a single set of parameters to be used for a particular model run. For this example we will use a simple SIS model to demonstrate how scenarios work. First, we set up the model as we would normally.

set.seed(10)

nw <- network_initialize(n = 200)
est <- netest(nw,
  formation = ~edges, target.stats = 60,
  coef.diss = dissolution_coefs(~offset(edges), 10, 0),
  verbose = FALSE
)
#> Starting maximum pseudolikelihood estimation (MPLE):
#> Obtaining the responsible dyads.
#> Evaluating the predictor and response matrix.
#> Maximizing the pseudolikelihood.
#> Finished MPLE.

param <- param.net(inf.prob = 0.9, rec.rate = 0.01, act.rate = 2)
init <- init.net(i.num = 10)
control <- control.net(type = "SIS", nsims = 1, nsteps = 250, verbose = FALSE)

Scenario Definitions

To define the scenarios, we will make use of the EpiModel::create_scenario_list function. It takes a specially formatted data.frame as input and outputs a list of scenarios usable by EpiModel.

We will use the tibble::tribble function to create the data.frame here. But any data frame construction methods will work as long as the resulting data.frame is properly formatted.

suppressMessages(library(dplyr))

scenarios.df <- tribble(
  ~.scenario.id, ~.at, ~inf.prob, ~rec.rate,
  "base", 0, 0.9, 0.01,
  "initial_change", 0, 0.2, 0.01,
  "multiple_changes", 0, 0.1, 0.04,
  "multiple_changes", 100, 0.9, 0.01,
  "multiple_changes", 200, 0.1, 0.1
)

knitr::kable(scenarios.df)

.scenario.id	.at	inf.prob	rec.rate
base	0	0.9	0.01
initial_change	0	0.2	0.01
multiple_changes	0	0.1	0.04
multiple_changes	100	0.9	0.01
multiple_changes	200	0.1	0.10

A data.frame of scenarios must be formatted as follows. First, there are two required columns: - .scenario.id: an identifier for the scenario - .at: when should the changes apply during the simulation

Any number of parameters columns. They must start with a letter and contain only letters, numbers or .. Underscores _ are not accepted. If a cell is left empty (NA), EpiModel will assume that you want to set the parameter to NA. NA does not mean that the value should remain unmodified.

In the data.frame above, three rows share the same .scenario.id. This means that EpiModel will consider it a single scenario were multiple events occur during the simulation.

To go from the scenarios.df to a list of usable scenarios we run:

scenarios.list <- create_scenario_list(scenarios.df)
str(scenarios.list, max.level = 2)
#> List of 3
#>  $ base            :List of 2
#>   ..$ id                 : chr "base"
#>   ..$ .param.updater.list:List of 1
#>  $ initial_change  :List of 2
#>   ..$ id                 : chr "initial_change"
#>   ..$ .param.updater.list:List of 1
#>  $ multiple_changes:List of 2
#>   ..$ id                 : chr "multiple_changes"
#>   ..$ .param.updater.list:List of 3

We now have a named list of scenarios. We will run all the scenarios, combine there results and plot the number of susceptible and infected over time to show what happened. To do so, we loop over all 3 scenarios and use EpiModel::use_scenario function to create a new sc.param object to be used for the simulation parameters.

# creation of a list that will hold the result of the simulations
d_list <- vector(mode = "list", length = length(scenarios.list))
names(d_list) <- names(scenarios.list)

for (scenario in scenarios.list) {
  # the id of the scenario is stored into `scenario$id`
  print(scenario$id)

  sc.param <- use_scenario(param, scenario)
  sim <- netsim(est, sc.param, init, control)
  # conversion to `data.frame` and storage of the scenario name in it
  d_sim <- as.data.frame(sim)
  d_sim[["scenario"]] <- scenario$id
  d_list[[scenario$id]] <- d_sim
}
#> [1] "base"
#> [1] "initial_change"
#> [1] "multiple_changes"
#> 
#>  A MESSAGE occured in module 'epimodel.internal' at step 100
#> 
#> 
#> At timestep = 100 the following parameters were modified:
#> 'inf.prob', 'rec.rate'
#> 
#>  A MESSAGE occured in module 'epimodel.internal' at step 200
#> 
#> 
#> At timestep = 200 the following parameters were modified:
#> 'inf.prob', 'rec.rate'

We see that for the “multiple_changes” scenarios, we received two messages, at time step 100 and 200, telling us that some parameters were changed during the simulation. The other scenarios were silent as the changes occurred before the simulation began.

Now we can merge and plot the results:

plot(d_list$base$time, d_list$base$i.num,
     type = "l", col = 1, lwd = 2, ylim = c(0, 250))
lines(d_list$initial_change$time, d_list$initial_change$i.num,
      type = "l", col = 2, lwd = 2)
lines(d_list$multiple_changes$time, d_list$multiple_changes$i.num,
      type = "l", col = 3, lwd = 2)
abline(v = c(100, 200), lty = 2)
legend("topleft", legend = names(d_list),
       col = 1:3, lwd = 2, cex = 0.9, bty = "n")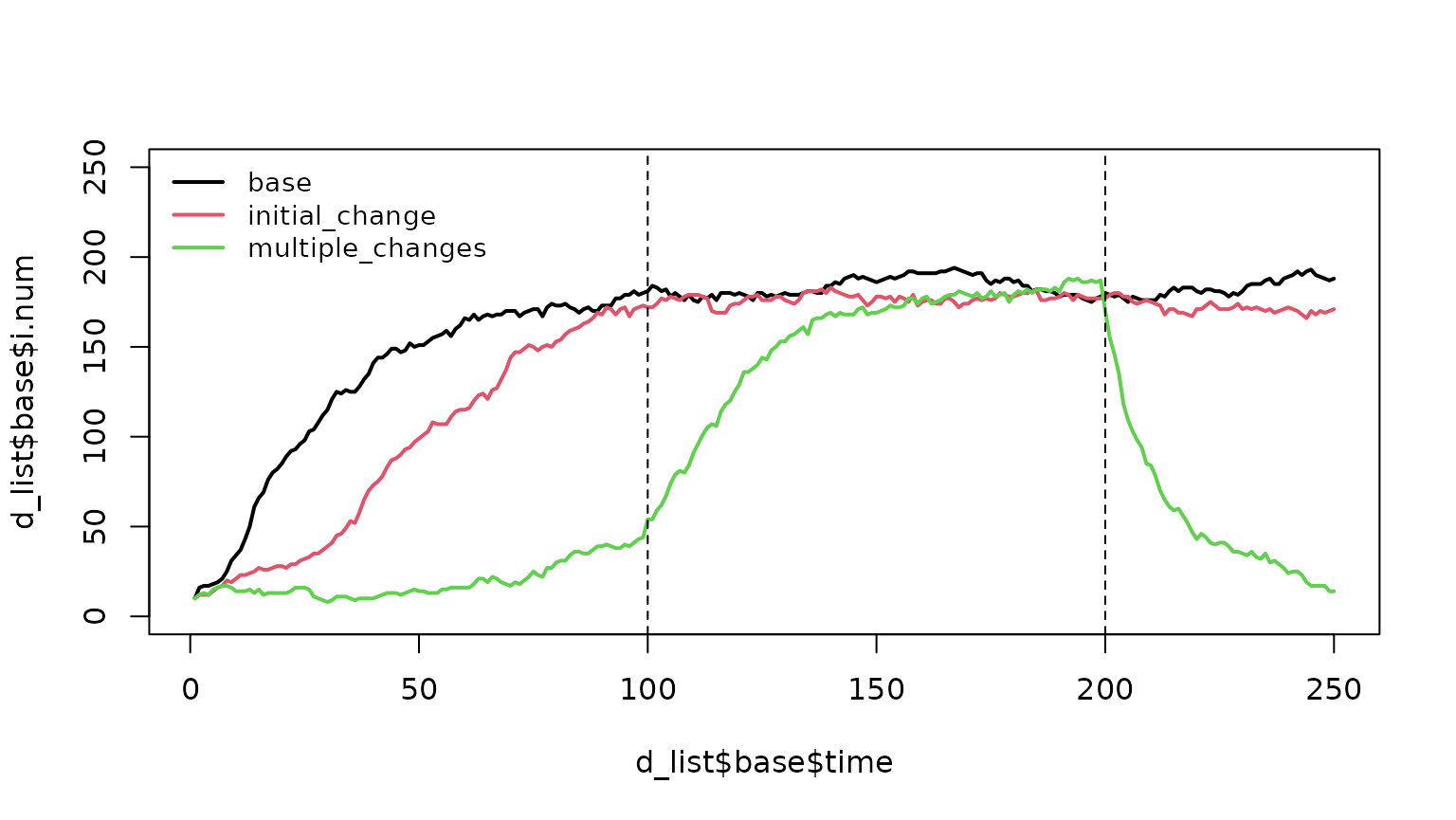

We can see that in the initial_change scenario, the epidemic speed is slower than in the base “scenario” as we have reduced the infection probability in the former.

The “multiple_changes” scenario shows different but expected results: - at first the epidemic is very slow as the infection probability is low and the recovery rate is high. - then at step 100, we apply the same values as in the “base” scenario. Thus the epidemic trajectory increases. - then at step 200, we reduce the infection probability and increase the recovery rate, which results in a quick epidemic extinction.

These scenarios are simplified to demonstrate the scenario system. Our research paper implementing the idea of multiple time-varying parameter changes was published in the Journal of Infectious Disease. The code can be found here.

Scenarios with Parameter Vectors

In full-scale modeling projects, we often have vectors of parameters. For example, we may have a parameter, hiv.test.rate, which is a vector of length 3 containing the weekly probabilities of HIV screening for Black, Hispanic or White persons, respectively.

For such parameters we can still use the scenarios approach described above. But in this case, we must define a column for each element of the modified parameter and end it with a numerical value for the order in which it lies in the vector: for example, \_1, \_2 and \_3 for the B, H, and W rates. Here is what that looks like:

scenarios.df <- tribble(
  ~.scenario.id, ~.at, ~hiv.test.rate_1, ~hiv.test.rate_2, ~hiv.test.rate_3,
  "base", 0, 0.001, 0.001, 0.001,
  "initial_change", 0, 0.002, 0.001, 0.002,
  "multiple_changes", 0, 0.002, 0.001, 0.002,
  "multiple_changes", 100, 0.004, 0.001, 0.004,
  "multiple_changes", 200, 0.008, 0.001, 0.008
)
knitr::kable(scenarios.df)

.scenario.id	.at	hiv.test.rate_1	hiv.test.rate_2	hiv.test.rate_3
base	0	0.001	0.001	0.001
initial_change	0	0.002	0.001	0.002
multiple_changes	0	0.002	0.001	0.002
multiple_changes	100	0.004	0.001	0.004
multiple_changes	200	0.008	0.001	0.008

One thing to note is that you must pass in the values for each sub-parameter in the scenarios.df. For example, even if the value of the HIV screening rate for Hispanic persons (the second value in the vector) is not changing across any scenarios, it is still necessary to define it as hiv.test.rate_2.

When working with a lot of parameters, it is recommended to store the scenarios.df as CSV or Excel file so your parameters can be easily shared and edited.

Parameters Input Via Table

Similar to the scenarios, the param.net function that creates the param object for netsim allows for inputting model parameters with a data.frame table. This allows a user to pass in many parameters at once, or work with a spreadsheet to track and update parameters before use in EpiModel.

The data.frame of parameters must be specifically formatted such that the first 3 columns must be: 1. ‘param’: The name of the parameter. If this is a non-scalar parameter (a vector of length > 1), end the parameter name with the position on the vector (e.g., "p_1", "p_2", …). 2. ‘value’: the value for the parameter (or the value of the parameter in the Nth position if non-scalar). 3. ‘type’: a character string containing either "numeric", "logical", or "character" to define the parameter object class.

In addition to these 3 columns, the data.frame can contain any number of other columns, such as details or source columns to document parameter meta-data. However, these extra columns will not be used by EpiModel.

In this example, we are inputting the parameters into a data.frame via tribble. In practice, parameters may be stored in an Excel file or CSV file and imported into a data.frame using the usual read functions.

df_params <- tribble(
  ~param, ~value, ~type,
  "hiv.test.rate_1",  "0.003",        "numeric",
  "hiv.test.rate_2",  "0.102",        "numeric",
  "hiv.test.rate_3",  "0.492",        "numeric",
  "prep.require.lnt", "TRUE",         "logical",
  "group_1",          "first",        "character",
  "group_2",          "second",       "character"
)
knitr::kable(df_params)

param	value	type
hiv.test.rate_1	0.003	numeric
hiv.test.rate_2	0.102	numeric
hiv.test.rate_3	0.492	numeric
prep.require.lnt	TRUE	logical
group_1	first	character
group_2	second	character

To use this table of parameters with param.net, pass in the table of parameters via the data.frame.params argument in param.net. Note that these parameters may also be combined with named parameters outside of a table, for maximum flexibility. In this example, we also pass in two extra parameters, other.param and act.rate. Note that when the param object is printed, all of the parameters are processed as expected.

param <- param.net(data.frame.params = df_params,
                   other.param = c(5, 10), act.rate = 1)
param
#> Fixed Parameters
#> ---------------------------
#> hiv.test.rate = 0.003 0.102 0.492
#> prep.require.lnt = TRUE
#> group = first second
#> act.rate = 1
#> other.param = 5 10

Random Parameters

We have demonstrated how to work with fixed and time-varying parameters above. One may also be interested in working with distributions of parameters that may follow some parametric or non-parametric form. For example, we may want to sample a range of values for the probability of infection given contact for each simulation of a model, instead of using a single value across all simulations.

The Model

EpiModel now includes functionality to input distributions of parameters for network models. We will demonstrate this with a simple SI model.

nw <- network_initialize(n = 50)

est <- netest(
  nw, formation = ~edges,
  target.stats = 25,
  coef.diss = dissolution_coefs(~offset(edges), 10, 0),
  verbose = FALSE
)
#> Starting maximum pseudolikelihood estimation (MPLE):
#> Obtaining the responsible dyads.
#> Evaluating the predictor and response matrix.
#> Maximizing the pseudolikelihood.
#> Finished MPLE.

param <- param.net(
  inf.prob = 0.3,
  act.rate = 0.5,
  dummy.param = 4,
  dummy.strat.param = c(0, 1)
)

init <- init.net(i.num = 10)
control <- control.net(type = "SI", nsims = 1, nsteps = 5, verbose = FALSE)
mod <- netsim(est, param, init, control)
mod
#> EpiModel Simulation
#> =======================
#> Model class: netsim
#> 
#> Simulation Summary
#> -----------------------
#> Model type: SI
#> No. simulations: 1
#> No. time steps: 5
#> No. NW groups: 1
#> 
#> Fixed Parameters
#> ---------------------------
#> inf.prob = 0.3
#> act.rate = 0.5
#> dummy.param = 4
#> dummy.strat.param = 0 1
#> groups = 1
#> 
#> Model Output
#> -----------------------
#> Variables: s.num i.num num si.flow
#> Networks: sim1
#> Transmissions: sim1
#> 
#> Formation Statistics
#> ----------------------- 
#>       Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
#> edges     25     16.8    -32.8  1.114  -7.364            NA          2.49
#> 
#> 
#> Duration Statistics
#> ----------------------- 
#>       Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
#> edges     10    8.697  -13.032   0.27  -4.819            NA         0.605
#> 
#> Dissolution Statistics
#> ----------------------- 
#>       Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
#> edges    0.1    0.065  -34.615  0.022  -1.608            NA         0.048

In the parameter list, we define four parameters: inf.prob, which will remain a single fixed value, but also act.rate, dummy.param, and dummy.strat.param, which here are fixed but will be defined below as random. The dummy.strat.param parameter has two elements; this vector approach may be used, for example, to stratify a parameter by subpopulation (e.g., as we did for the race-stratified HIV screening rate example above). The last line prints a summary of the model object. We can see the value of the parameters under the “Fixed Parameters” section. Note the additional groups parameter defined automatically by EpiModel as part of the “SI” model definition.

Adding Random Parameters

To allow our parameters to be drawn from a distribution of random values, we use the random.params argument to param.net. There are two ways of defining which parameters are random, and the distribution of values for those random parameters to draw randomly and how to draw them.

Generator Functions

The first option is to define a generator function for each parameter we want to declare as random.

my.randoms <- list(
  act.rate = param_random(c(0.25, 0.5, 0.75)),
  dummy.param = function() rbeta(1, 1, 2),
  dummy.strat.param = function() {
    c(rnorm(1, 0.05, 0.01),
      rnorm(1, 0.15, 0.03))
  }
)

param <- param.net(
  inf.prob = 0.3,
  random.params = my.randoms
)

param
#> Fixed Parameters
#> ---------------------------
#> inf.prob = 0.3
#> 
#> Random Parameters
#> (Not drawn yet)
#> ---------------------------
#> act.rate = <function>
#> dummy.param = <function>
#> dummy.strat.param = <function>

We kept the inf.prob parameter fixed at 0.3, and then defined a list object called my.randoms containing 3 elements:

act.rate uses the param_random function factory defined by EpiModel (see ?EpiModel::param_random). In this case, each simulation will sample one of the three defined values in the vector with equal probability.
dummy.param is a function with no argument that returns a random value from a beta distribution.
dummy.strat.param is a function with no argument that returns 2 values sampled from normal distributions, each with different means and standard deviations.

Each element is named after the parameter it will fill and MUST BE a function taking no argument and outputting a vector of the right size for the parameter: size 1 for act.rate and dummy.param; size 2 for dummy.strat.param. Note that when we print out the parameter list before running the model, it includes the random parameter definitions as functions, as their sampled values are not yet realized.

The rest of the model is then run as before, although we increase the simulation count to three to demonstrate the parameter stochasticity.

control <- control.net(type = "SI", nsims = 3, nsteps = 5, verbose = FALSE)
mod <- netsim(est, param, init, control)

mod
#> EpiModel Simulation
#> =======================
#> Model class: netsim
#> 
#> Simulation Summary
#> -----------------------
#> Model type: SI
#> No. simulations: 3
#> No. time steps: 5
#> No. NW groups: 1
#> 
#> Fixed Parameters
#> ---------------------------
#> inf.prob = 0.3
#> groups = 1
#> 
#> Random Parameters
#> ---------------------------
#> act.rate = 0.5 0.75 0.25
#> dummy.param = 0.5293276 0.2734432 0.11582
#> dummy.strat.param = <list>
#> 
#> Model Output
#> -----------------------
#> Variables: s.num i.num num si.flow
#> Networks: sim1 ... sim3
#> Transmissions: sim1 ... sim3
#> 
#> Formation Statistics
#> ----------------------- 
#>       Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
#> edges     25   21.667  -13.333  1.022  -3.262          4.46         3.958
#> 
#> 
#> Duration Statistics
#> ----------------------- 
#>       Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
#> edges     10    8.977  -10.226  0.387  -2.642         1.593         1.499
#> 
#> Dissolution Statistics
#> ----------------------- 
#>       Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
#> edges    0.1    0.114   13.774  0.015   0.938         0.029         0.057

After running 3 simulations we can see that the inf.prob is still displayed under the “Fixed Parameters” section. The other three parameters are displayed under the “Random Parameters” section: act.rate and dummy.param now have 3 values associated with them, one per simulation. dummy.strat.param have <list> as its value because each simulation has a vector of size 2.

To more easily inspect the parameter values, we can use the get_param_set function:

all.params <- get_param_set(mod)
all.params
#>   sim inf.prob vital groups act.rate dummy.param dummy.strat.param_1
#> 1   1      0.3 FALSE      1     0.50   0.5293276          0.05392462
#> 2   2      0.3 FALSE      1     0.75   0.2734432          0.04759042
#> 3   3      0.3 FALSE      1     0.25   0.1158200          0.05619374
#>   dummy.strat.param_2
#> 1           0.1511654
#> 2           0.1293028
#> 3           0.1918158

These parameters can then be merged with the epidemic data, for easy analysis of the relationship between parameters and outputs:

epi <- as.data.frame(mod)
left_join(epi, all.params)
#> Joining with `by = join_by(sim)`
#>    sim time s.num i.num num si.flow inf.prob vital groups act.rate dummy.param
#> 1    1    1    40    10  50      NA      0.3 FALSE      1     0.50   0.5293276
#> 2    1    2    40    10  50       0      0.3 FALSE      1     0.50   0.5293276
#> 3    1    3    36    14  50       4      0.3 FALSE      1     0.50   0.5293276
#> 4    1    4    34    16  50       2      0.3 FALSE      1     0.50   0.5293276
#> 5    1    5    34    16  50       0      0.3 FALSE      1     0.50   0.5293276
#> 6    2    1    40    10  50      NA      0.3 FALSE      1     0.75   0.2734432
#> 7    2    2    39    11  50       1      0.3 FALSE      1     0.75   0.2734432
#> 8    2    3    38    12  50       1      0.3 FALSE      1     0.75   0.2734432
#> 9    2    4    36    14  50       2      0.3 FALSE      1     0.75   0.2734432
#> 10   2    5    36    14  50       0      0.3 FALSE      1     0.75   0.2734432
#> 11   3    1    40    10  50      NA      0.3 FALSE      1     0.25   0.1158200
#> 12   3    2    40    10  50       0      0.3 FALSE      1     0.25   0.1158200
#> 13   3    3    40    10  50       0      0.3 FALSE      1     0.25   0.1158200
#> 14   3    4    40    10  50       0      0.3 FALSE      1     0.25   0.1158200
#> 15   3    5    39    11  50       1      0.3 FALSE      1     0.25   0.1158200
#>    dummy.strat.param_1 dummy.strat.param_2
#> 1           0.05392462           0.1511654
#> 2           0.05392462           0.1511654
#> 3           0.05392462           0.1511654
#> 4           0.05392462           0.1511654
#> 5           0.05392462           0.1511654
#> 6           0.04759042           0.1293028
#> 7           0.04759042           0.1293028
#> 8           0.04759042           0.1293028
#> 9           0.04759042           0.1293028
#> 10          0.04759042           0.1293028
#> 11          0.05619374           0.1918158
#> 12          0.05619374           0.1918158
#> 13          0.05619374           0.1918158
#> 14          0.05619374           0.1918158
#> 15          0.05619374           0.1918158

Parameter Sets

The drawback of generator function approach above is that it cannot produce correlated parameter sets. For instance, we may want dummy.param and dummy.strat.param to be related to one another within a single simulation. We might also use an external method for generating parameter sets, such as Latin hypercube sampling of multiple parameters.

For this, we need to pre-define a data.frame of parameter values. In this example, we have five parameter sets:

n <- 5

related.param <- data.frame(
  dummy.param = rbeta(n, 1, 2)
)

related.param$dummy.strat.param_1 <- related.param$dummy.param + rnorm(n)
related.param$dummy.strat.param_2 <- related.param$dummy.param * 2 + rnorm(n)

related.param
#>   dummy.param dummy.strat.param_1 dummy.strat.param_2
#> 1  0.40042189           1.6831189           1.0748786
#> 2  0.73021770           2.3839536           1.3420617
#> 3  0.05306671           0.6405278          -0.7281755
#> 4  0.90490846          -1.3179645          -0.4500947
#> 5  0.48049243           0.7020599           2.3109663

We now have a data.frame with 5 rows and 3 columns. Each row contains a set of parameters values that will be used together in a single simulation of the model. This way we keep the relationship between each value.

The first column of the data.frame is named dummy.param, similar to the name of the parameter. For dummy.start.param we need two columns as the parameter contains two values. To achieve this, we name the two columns dummy.start.param_1 and dummy.strat.param_2. The value after the underscore informs EpiModel how it should combine these values into a vector (note that this uses the same syntax as with stratified parameters within model scenarios described above). This in turn means that the underscore symbol is not allowed in proper parameter names.

Then we set up the rest of the parameters. related.param is saved in the my.randoms list under the special reserved name param.random.set.

my.randoms <- list(
  act.rate = param_random(c(0.25, 0.5, 0.75)),
  param.random.set = related.param

)

param <- param.net(
  inf.prob = 0.3,
  random.params = my.randoms
)

param
#> Fixed Parameters
#> ---------------------------
#> inf.prob = 0.3
#> 
#> Random Parameters
#> (Not drawn yet)
#> ---------------------------
#> act.rate = <function>
#> param.random.set = <data.frame> ( dimensions: 5 3 )

The inf.prob parameter remains fixed, the act.rate parameter remains random with independent sample, but now a set of the two remaining parameters is passed in as correlated parameters with param.random_set.

control <- control.net(type = "SI", nsims = 3, nsteps = 5, verbose = FALSE)
mod <- netsim(est, param, init, control)

mod
#> EpiModel Simulation
#> =======================
#> Model class: netsim
#> 
#> Simulation Summary
#> -----------------------
#> Model type: SI
#> No. simulations: 3
#> No. time steps: 5
#> No. NW groups: 1
#> 
#> Fixed Parameters
#> ---------------------------
#> inf.prob = 0.3
#> groups = 1
#> 
#> Random Parameters
#> ---------------------------
#> dummy.param = 0.9049085 0.4804924 0.4004219
#> dummy.strat.param = <list>
#> act.rate = 0.75 0.75 0.75
#> 
#> Model Output
#> -----------------------
#> Variables: s.num i.num num si.flow
#> Networks: sim1 ... sim3
#> Transmissions: sim1 ... sim3
#> 
#> Formation Statistics
#> ----------------------- 
#>       Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
#> edges     25   25.933    3.733  0.502   1.859         0.757         1.944
#> 
#> 
#> Duration Statistics
#> ----------------------- 
#>       Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
#> edges     10    9.584   -4.158  0.183  -2.275          0.68         0.708
#> 
#> Dissolution Statistics
#> ----------------------- 
#>       Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
#> edges    0.1    0.114    14.49  0.011    1.27         0.022         0.044

The output is similar to what we saw with the generator functions defined above. See that the correlated parameter sets are sampled from together from the data frame of parameters.

related.param
#>   dummy.param dummy.strat.param_1 dummy.strat.param_2
#> 1  0.40042189           1.6831189           1.0748786
#> 2  0.73021770           2.3839536           1.3420617
#> 3  0.05306671           0.6405278          -0.7281755
#> 4  0.90490846          -1.3179645          -0.4500947
#> 5  0.48049243           0.7020599           2.3109663
get_param_set(mod)
#>   sim inf.prob vital groups dummy.param dummy.strat.param_1 dummy.strat.param_2
#> 1   1      0.3 FALSE      1   0.9049085          -1.3179645          -0.4500947
#> 2   2      0.3 FALSE      1   0.4804924           0.7020599           2.3109663
#> 3   3      0.3 FALSE      1   0.4004219           1.6831189           1.0748786
#>   act.rate
#> 1     0.75
#> 2     0.75
#> 3     0.75

Time-Varying Parameters and Control Settings (Advanced)

Within EpiModel, the scenarios described above uses an updater module to implement parameter changes at a given time step. This section describes how these mechanisms function and how to use them directly if the scenarios approach above is not flexible enough, or if you would also like to have time-varying control settings.

Parameter Updaters

To define what parameters should change and when during the simulation, we need to define updater lists. An updater is a list with two named elements: at, the time step when the change will take place, and param a named list of parameters to update. For example:

list(
  at = 10,
  param = list(
    inf.prob = 0.3,
    act.rate = 0.5
  )
)
#> $at
#> [1] 10
#> 
#> $param
#> $param$inf.prob
#> [1] 0.3
#> 
#> $param$act.rate
#> [1] 0.5

This defines an updater that will change the value of the inf.prob parameter to 0.3 and the value to the act.rate parameter to 0.5. This change will happen at time step 10. If we want, multiple parameter changes, then we can write a list of updaters:

# Create a `list.of.updaters`
list.of.updaters <- list(
  # this is one updater
  list(
    at = 100,
    param = list(
      inf.prob = 0.3,
      act.rate = 0.3
    )
  ),
  # this is another updater
  list(
    at = 125,
    param = list(
      inf.prob = 0.01
    )
  )
)

In this example, we define two updaters, one that occurs at time step 100 and the other one at time step 125. As demonstrated below, these values for inf.prob and act.rate will change from the values of 0.1 established by param.netat the beginning of the time series.

Incorporating Updaters

Below we set up a complete example with a closed population SI model using the parameters and updaters defined above. Note that the parameter updaters get passed into param.net with the special .param.updater.list argument.

param <- param.net(
 inf.prob = 0.1,
 act.rate = 0.1,
 .param.updater.list = list.of.updaters
)
init <- init.net(i.num = 10)
control <- control.net(
 type = "SI",
 nsims = 1,
 nsteps = 200,
 verbose = FALSE
)

Next, we run the model with a simple network structure:

nw <- network_initialize(n = 100)
est <- netest(
  nw,
  formation = ~edges,
  target.stats = 50,
  coef.diss = dissolution_coefs(~offset(edges), 10, 0),
  verbose = FALSE
)
#> Starting maximum pseudolikelihood estimation (MPLE):
#> Obtaining the responsible dyads.
#> Evaluating the predictor and response matrix.
#> Maximizing the pseudolikelihood.
#> Finished MPLE.
mod <- netsim(est, param, init, control)
#> 
#>  A MESSAGE occured in module 'epimodel.internal' at step 100
#> 
#> 
#> At timestep = 100 the following parameters were modified:
#> 'inf.prob', 'act.rate'
#> 
#>  A MESSAGE occured in module 'epimodel.internal' at step 125
#> 
#> 
#> At timestep = 125 the following parameters were modified:
#> 'inf.prob'

The model plot here demonstrates the inflection points in the epidemic trajectory at the two parameter change points defined above.

plot(mod, mean.smooth = FALSE)
abline(v = c(100, 125), lty = 2, col = "grey50")

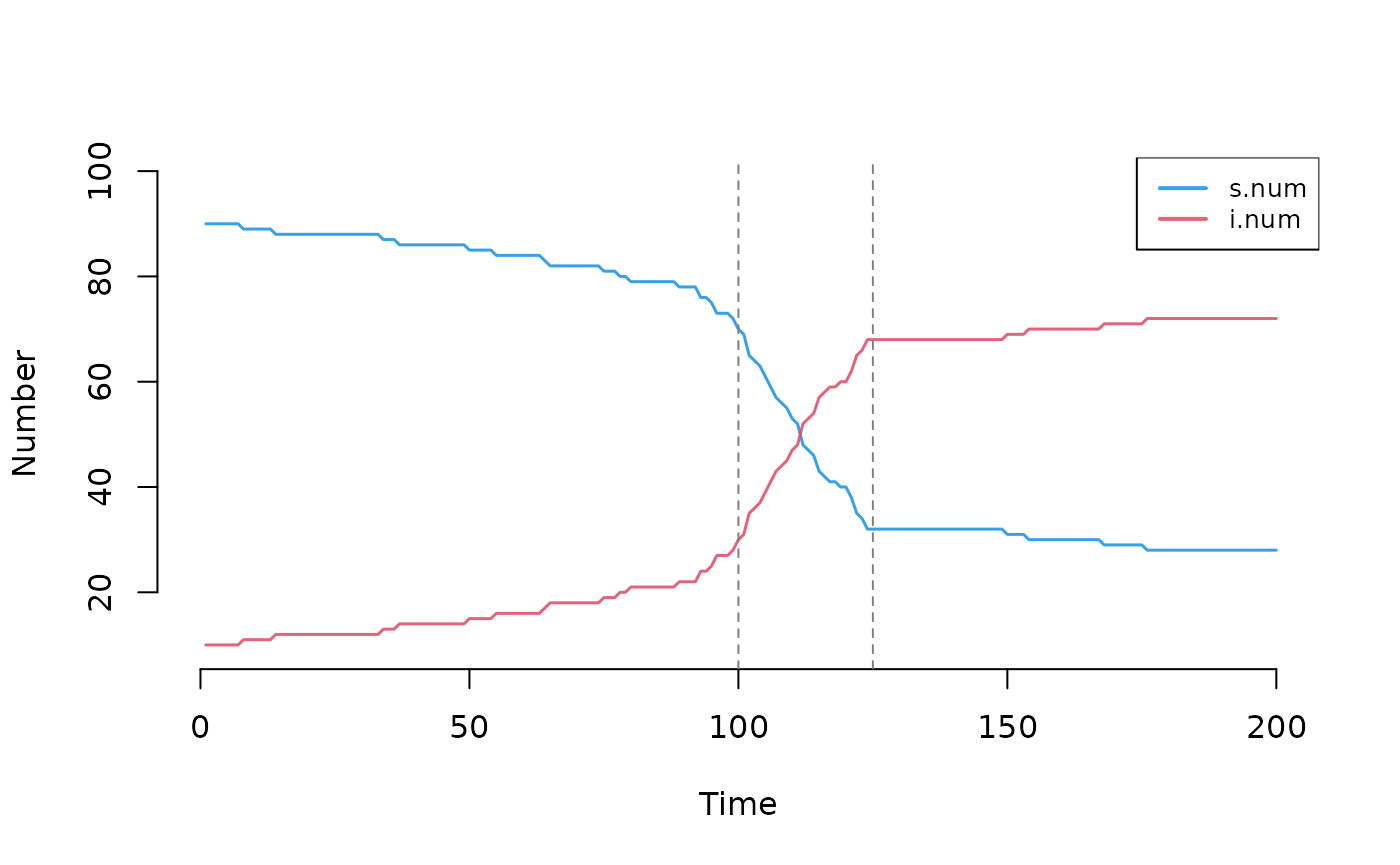
Verbosity

When creating a parameter updater, one can add an optional verbose element to the list. If TRUE, EpiModel will output a message` describing what changes were performed and when they occurred.

list(
  at = 10,
  param = list(
    inf.prob = 0.3,
    act.rate = 0.5
  ),
  verbose = TRUE
)
#> $at
#> [1] 10
#> 
#> $param
#> $param$inf.prob
#> [1] 0.3
#> 
#> $param$act.rate
#> [1] 0.5
#> 
#> 
#> $verbose
#> [1] TRUE

Relative Parameter Changes

It may be useful to configure the changes with respect to the current value instead of a fixed new value. This is possible as demonstrated below for inf.prob.

list(
  at = 10,
  param = list(
    inf.prob = function(x) plogis(qlogis(x) + log(2)),
    act.rate = 0.5
  )
)
#> $at
#> [1] 10
#> 
#> $param
#> $param$inf.prob
#> function (x) 
#> plogis(qlogis(x) + log(2))
#> 
#> $param$act.rate
#> [1] 0.5

This updater will set the value of act.rate to 0.5 as before. But, for inf.prob we define a function (not a function call). In this case, the will apply the function to the current value of act.rate. If we consider as in the previous example that act.rate is set to 0.1 by param.net, then its new value will be obtained by adding the log odds of 2 to the original value of inf.prob: plogis(qlogis(0.1) + log(2)): 0.1818182. Whereas the previous value of inf.prob was 0.10, the updated value will be 0.18.

Time-Varying Control Settings

Similar to time-varying parameters, we can use time-varying controls. These work in the same way. Each control updater is defined as a list of lists.

# Create a `list.of.updaters`
list.of.updaters <- list(
  # this is one updater
  list(
    at = 100,
    control = list(
      resimulate.network = FALSE
    )
  ),
  # this is another updater
  list(
    at = 125,
    control = list(
      verbose = FALSE
    )
  )
)

This example sets two control updaters, one that turns off network resimulation at timestep 100 and another toggling of the model verbosity at step 125.

The list.of.updaters then gets passed into control.net through the special .control.updater.list argument.

control <- control.net(
 type = "SI",
 nsims = 1,
 nsteps = 200,
 verbose = TRUE,
 .control.updater.list = list.of.updaters
)

EpiModel v2.5.0

2024-11-05