Inspired by dplyr::mutate, mutate_epi adds new
variables to the epidemiological and related variables within
simulated model objects of any class in EpiModel.
Examples
# DCM example
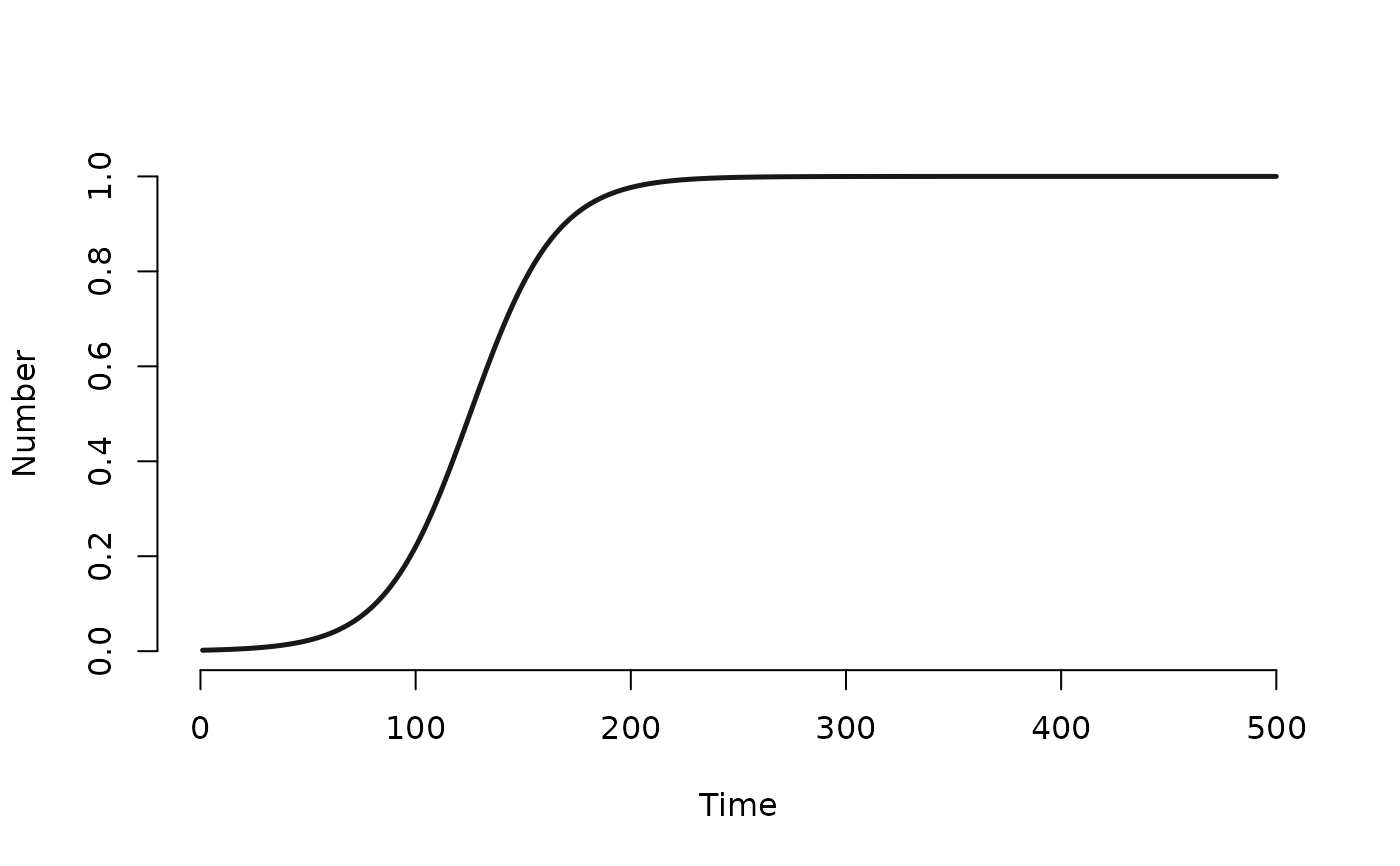
param <- param.dcm(inf.prob = 0.2, act.rate = 0.25)
init <- init.dcm(s.num = 500, i.num = 1)
control <- control.dcm(type = "SI", nsteps = 500)
mod1 <- dcm(param, init, control)
mod1 <- mutate_epi(mod1, prev = i.num/num)
plot(mod1, y = "prev")
 # Network model example
nw <- network_initialize(n = 100)
nw <- set_vertex_attribute(nw, "group", rep(1:2, each = 50))
formation <- ~edges
target.stats <- 50
coef.diss <- dissolution_coefs(dissolution = ~offset(edges), duration = 20)
est1 <- netest(nw, formation, target.stats, coef.diss, verbose = FALSE)
#> Starting simulated annealing (SAN)
#> Iteration 1 of at most 4
#> Finished simulated annealing
#> Starting maximum pseudolikelihood estimation (MPLE):
#> Obtaining the responsible dyads.
#> Evaluating the predictor and response matrix.
#> Maximizing the pseudolikelihood.
#> Finished MPLE.
param <- param.net(inf.prob = 0.3, inf.prob.g2 = 0.15)
init <- init.net(i.num = 1, i.num.g2 = 0)
control <- control.net(type = "SI", nsteps = 10, nsims = 3,
verbose = FALSE)
mod1 <- netsim(est1, param, init, control)
mod1
#> EpiModel Simulation
#> =======================
#> Model class: netsim
#>
#> Simulation Summary
#> -----------------------
#> Model type: SI
#> No. simulations: 3
#> No. time steps: 10
#> No. NW groups: 2
#>
#> Fixed Parameters
#> ---------------------------
#> inf.prob = 0.3
#> inf.prob.g2 = 0.15
#> act.rate = 1
#> groups = 2
#>
#> Model Output
#> -----------------------
#> Variables: s.num i.num num s.num.g2 i.num.g2 num.g2
#> si.flow si.flow.g2
#> Networks: sim1 ... sim3
#> Transmissions: sim1 ... sim3
#>
#> Formation Statistics
#> -----------------------
#> Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
#> edges 50 53 6 2.658 1.129 13.99 12.214
#>
#>
#> Duration Statistics
#> -----------------------
#> Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
#> edges 20 22.053 10.263 0.55 3.732 1.639 1.9
#>
#> Dissolution Statistics
#> -----------------------
#> Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
#> edges 0.05 0.043 -14.015 0.003 -2.283 0.012 0.025
#>
# Add the prevalences to the dataset
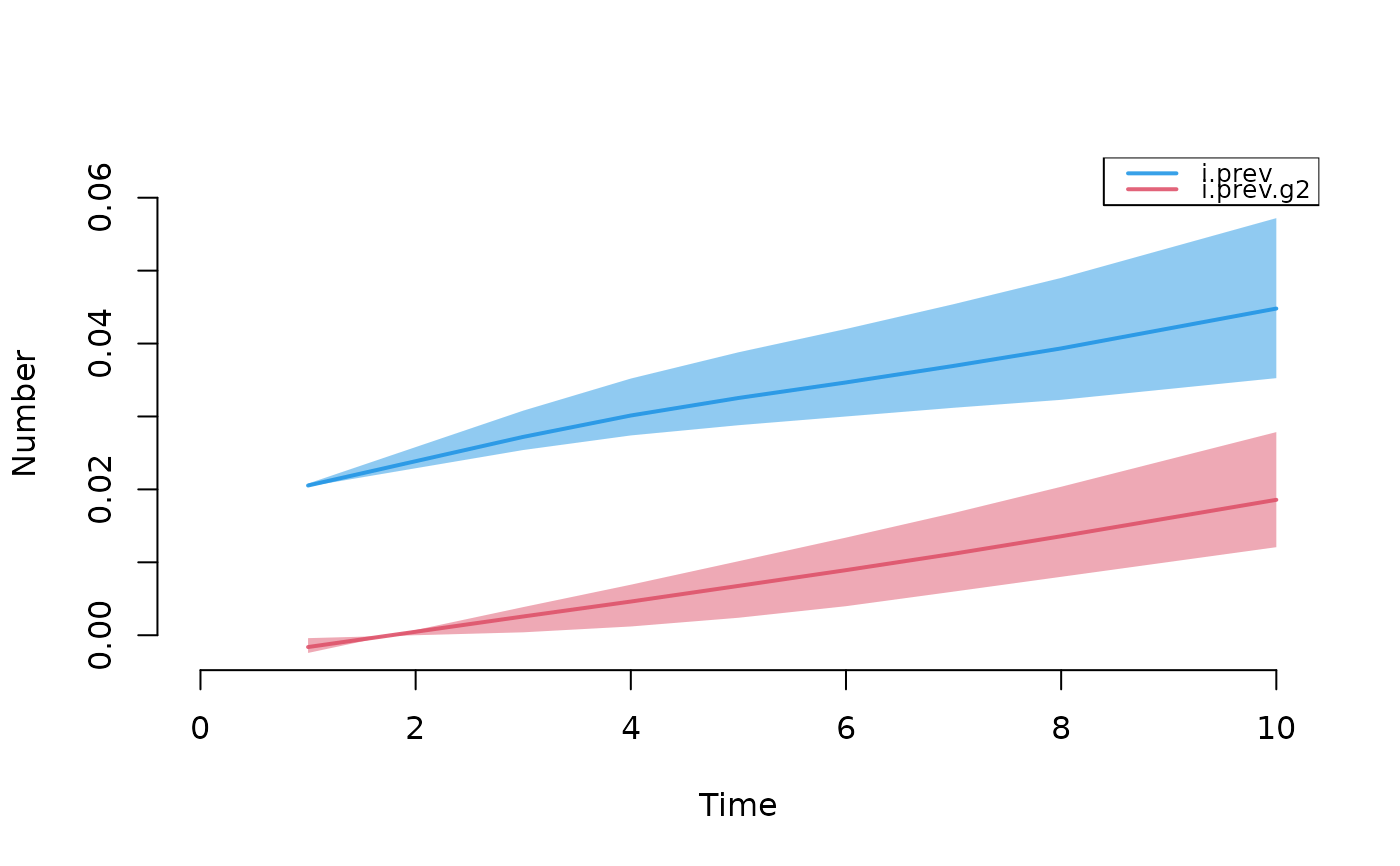
mod1 <- mutate_epi(mod1, i.prev = i.num / num,
i.prev.g2 = i.num.g2 / num.g2)
plot(mod1, y = c("i.prev", "i.prev.g2"), qnts = 0.5, legend = TRUE)
# Network model example
nw <- network_initialize(n = 100)
nw <- set_vertex_attribute(nw, "group", rep(1:2, each = 50))
formation <- ~edges
target.stats <- 50
coef.diss <- dissolution_coefs(dissolution = ~offset(edges), duration = 20)
est1 <- netest(nw, formation, target.stats, coef.diss, verbose = FALSE)
#> Starting simulated annealing (SAN)
#> Iteration 1 of at most 4
#> Finished simulated annealing
#> Starting maximum pseudolikelihood estimation (MPLE):
#> Obtaining the responsible dyads.
#> Evaluating the predictor and response matrix.
#> Maximizing the pseudolikelihood.
#> Finished MPLE.
param <- param.net(inf.prob = 0.3, inf.prob.g2 = 0.15)
init <- init.net(i.num = 1, i.num.g2 = 0)
control <- control.net(type = "SI", nsteps = 10, nsims = 3,
verbose = FALSE)
mod1 <- netsim(est1, param, init, control)
mod1
#> EpiModel Simulation
#> =======================
#> Model class: netsim
#>
#> Simulation Summary
#> -----------------------
#> Model type: SI
#> No. simulations: 3
#> No. time steps: 10
#> No. NW groups: 2
#>
#> Fixed Parameters
#> ---------------------------
#> inf.prob = 0.3
#> inf.prob.g2 = 0.15
#> act.rate = 1
#> groups = 2
#>
#> Model Output
#> -----------------------
#> Variables: s.num i.num num s.num.g2 i.num.g2 num.g2
#> si.flow si.flow.g2
#> Networks: sim1 ... sim3
#> Transmissions: sim1 ... sim3
#>
#> Formation Statistics
#> -----------------------
#> Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
#> edges 50 53 6 2.658 1.129 13.99 12.214
#>
#>
#> Duration Statistics
#> -----------------------
#> Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
#> edges 20 22.053 10.263 0.55 3.732 1.639 1.9
#>
#> Dissolution Statistics
#> -----------------------
#> Target Sim Mean Pct Diff Sim SE Z Score SD(Sim Means) SD(Statistic)
#> edges 0.05 0.043 -14.015 0.003 -2.283 0.012 0.025
#>
# Add the prevalences to the dataset
mod1 <- mutate_epi(mod1, i.prev = i.num / num,
i.prev.g2 = i.num.g2 / num.g2)
plot(mod1, y = c("i.prev", "i.prev.g2"), qnts = 0.5, legend = TRUE)
 # Add incidence rate per 100 person years (assume time step = 1 week)
mod1 <- mutate_epi(mod1, ir100 = 5200*(si.flow + si.flow.g2) /
(s.num + s.num.g2))
as.data.frame(mod1)
#> sim time s.num i.num num s.num.g2 i.num.g2 num.g2 si.flow si.flow.g2 i.prev
#> 1 1 1 49 1 50 50 0 50 NA NA 0.02
#> 2 1 2 49 1 50 50 0 50 0 0 0.02
#> 3 1 3 49 1 50 50 0 50 0 0 0.02
#> 4 1 4 49 1 50 50 0 50 0 0 0.02
#> 5 1 5 49 1 50 50 0 50 0 0 0.02
#> 6 1 6 48 2 50 50 0 50 1 0 0.04
#> 7 1 7 47 3 50 50 0 50 1 0 0.06
#> 8 1 8 47 3 50 50 0 50 0 0 0.06
#> 9 1 9 47 3 50 50 0 50 0 0 0.06
#> 10 1 10 47 3 50 50 0 50 0 0 0.06
#> 11 2 1 49 1 50 50 0 50 NA NA 0.02
#> 12 2 2 49 1 50 50 0 50 0 0 0.02
#> 13 2 3 48 2 50 50 0 50 1 0 0.04
#> 14 2 4 48 2 50 50 0 50 0 0 0.04
#> 15 2 5 48 2 50 50 0 50 0 0 0.04
#> 16 2 6 48 2 50 50 0 50 0 0 0.04
#> 17 2 7 48 2 50 50 0 50 0 0 0.04
#> 18 2 8 48 2 50 50 0 50 0 0 0.04
#> 19 2 9 48 2 50 50 0 50 0 0 0.04
#> 20 2 10 48 2 50 50 0 50 0 0 0.04
#> 21 3 1 49 1 50 50 0 50 NA NA 0.02
#> 22 3 2 49 1 50 50 0 50 0 0 0.02
#> 23 3 3 49 1 50 50 0 50 0 0 0.02
#> 24 3 4 49 1 50 50 0 50 0 0 0.02
#> 25 3 5 49 1 50 50 0 50 0 0 0.02
#> 26 3 6 49 1 50 50 0 50 0 0 0.02
#> 27 3 7 49 1 50 50 0 50 0 0 0.02
#> 28 3 8 49 1 50 50 0 50 0 0 0.02
#> 29 3 9 49 1 50 50 0 50 0 0 0.02
#> 30 3 10 49 1 50 50 0 50 0 0 0.02
#> i.prev.g2 ir100
#> 1 0 NA
#> 2 0 0.00000
#> 3 0 0.00000
#> 4 0 0.00000
#> 5 0 0.00000
#> 6 0 53.06122
#> 7 0 53.60825
#> 8 0 0.00000
#> 9 0 0.00000
#> 10 0 0.00000
#> 11 0 NA
#> 12 0 0.00000
#> 13 0 53.06122
#> 14 0 0.00000
#> 15 0 0.00000
#> 16 0 0.00000
#> 17 0 0.00000
#> 18 0 0.00000
#> 19 0 0.00000
#> 20 0 0.00000
#> 21 0 NA
#> 22 0 0.00000
#> 23 0 0.00000
#> 24 0 0.00000
#> 25 0 0.00000
#> 26 0 0.00000
#> 27 0 0.00000
#> 28 0 0.00000
#> 29 0 0.00000
#> 30 0 0.00000
as.data.frame(mod1, out = "mean")
#> time s.num i.num num s.num.g2 i.num.g2 num.g2 si.flow si.flow.g2
#> 1 1 49.00000 1.000000 50 50 0 50 NaN NaN
#> 2 2 49.00000 1.000000 50 50 0 50 0.0000000 0
#> 3 3 48.66667 1.333333 50 50 0 50 0.3333333 0
#> 4 4 48.66667 1.333333 50 50 0 50 0.0000000 0
#> 5 5 48.66667 1.333333 50 50 0 50 0.0000000 0
#> 6 6 48.33333 1.666667 50 50 0 50 0.3333333 0
#> 7 7 48.00000 2.000000 50 50 0 50 0.3333333 0
#> 8 8 48.00000 2.000000 50 50 0 50 0.0000000 0
#> 9 9 48.00000 2.000000 50 50 0 50 0.0000000 0
#> 10 10 48.00000 2.000000 50 50 0 50 0.0000000 0
#> i.prev i.prev.g2 ir100
#> 1 0.02000000 0 NaN
#> 2 0.02000000 0 0.00000
#> 3 0.02666667 0 17.68707
#> 4 0.02666667 0 0.00000
#> 5 0.02666667 0 0.00000
#> 6 0.03333333 0 17.68707
#> 7 0.04000000 0 17.86942
#> 8 0.04000000 0 0.00000
#> 9 0.04000000 0 0.00000
#> 10 0.04000000 0 0.00000
# Add incidence rate per 100 person years (assume time step = 1 week)
mod1 <- mutate_epi(mod1, ir100 = 5200*(si.flow + si.flow.g2) /
(s.num + s.num.g2))
as.data.frame(mod1)
#> sim time s.num i.num num s.num.g2 i.num.g2 num.g2 si.flow si.flow.g2 i.prev
#> 1 1 1 49 1 50 50 0 50 NA NA 0.02
#> 2 1 2 49 1 50 50 0 50 0 0 0.02
#> 3 1 3 49 1 50 50 0 50 0 0 0.02
#> 4 1 4 49 1 50 50 0 50 0 0 0.02
#> 5 1 5 49 1 50 50 0 50 0 0 0.02
#> 6 1 6 48 2 50 50 0 50 1 0 0.04
#> 7 1 7 47 3 50 50 0 50 1 0 0.06
#> 8 1 8 47 3 50 50 0 50 0 0 0.06
#> 9 1 9 47 3 50 50 0 50 0 0 0.06
#> 10 1 10 47 3 50 50 0 50 0 0 0.06
#> 11 2 1 49 1 50 50 0 50 NA NA 0.02
#> 12 2 2 49 1 50 50 0 50 0 0 0.02
#> 13 2 3 48 2 50 50 0 50 1 0 0.04
#> 14 2 4 48 2 50 50 0 50 0 0 0.04
#> 15 2 5 48 2 50 50 0 50 0 0 0.04
#> 16 2 6 48 2 50 50 0 50 0 0 0.04
#> 17 2 7 48 2 50 50 0 50 0 0 0.04
#> 18 2 8 48 2 50 50 0 50 0 0 0.04
#> 19 2 9 48 2 50 50 0 50 0 0 0.04
#> 20 2 10 48 2 50 50 0 50 0 0 0.04
#> 21 3 1 49 1 50 50 0 50 NA NA 0.02
#> 22 3 2 49 1 50 50 0 50 0 0 0.02
#> 23 3 3 49 1 50 50 0 50 0 0 0.02
#> 24 3 4 49 1 50 50 0 50 0 0 0.02
#> 25 3 5 49 1 50 50 0 50 0 0 0.02
#> 26 3 6 49 1 50 50 0 50 0 0 0.02
#> 27 3 7 49 1 50 50 0 50 0 0 0.02
#> 28 3 8 49 1 50 50 0 50 0 0 0.02
#> 29 3 9 49 1 50 50 0 50 0 0 0.02
#> 30 3 10 49 1 50 50 0 50 0 0 0.02
#> i.prev.g2 ir100
#> 1 0 NA
#> 2 0 0.00000
#> 3 0 0.00000
#> 4 0 0.00000
#> 5 0 0.00000
#> 6 0 53.06122
#> 7 0 53.60825
#> 8 0 0.00000
#> 9 0 0.00000
#> 10 0 0.00000
#> 11 0 NA
#> 12 0 0.00000
#> 13 0 53.06122
#> 14 0 0.00000
#> 15 0 0.00000
#> 16 0 0.00000
#> 17 0 0.00000
#> 18 0 0.00000
#> 19 0 0.00000
#> 20 0 0.00000
#> 21 0 NA
#> 22 0 0.00000
#> 23 0 0.00000
#> 24 0 0.00000
#> 25 0 0.00000
#> 26 0 0.00000
#> 27 0 0.00000
#> 28 0 0.00000
#> 29 0 0.00000
#> 30 0 0.00000
as.data.frame(mod1, out = "mean")
#> time s.num i.num num s.num.g2 i.num.g2 num.g2 si.flow si.flow.g2
#> 1 1 49.00000 1.000000 50 50 0 50 NaN NaN
#> 2 2 49.00000 1.000000 50 50 0 50 0.0000000 0
#> 3 3 48.66667 1.333333 50 50 0 50 0.3333333 0
#> 4 4 48.66667 1.333333 50 50 0 50 0.0000000 0
#> 5 5 48.66667 1.333333 50 50 0 50 0.0000000 0
#> 6 6 48.33333 1.666667 50 50 0 50 0.3333333 0
#> 7 7 48.00000 2.000000 50 50 0 50 0.3333333 0
#> 8 8 48.00000 2.000000 50 50 0 50 0.0000000 0
#> 9 9 48.00000 2.000000 50 50 0 50 0.0000000 0
#> 10 10 48.00000 2.000000 50 50 0 50 0.0000000 0
#> i.prev i.prev.g2 ir100
#> 1 0.02000000 0 NaN
#> 2 0.02000000 0 0.00000
#> 3 0.02666667 0 17.68707
#> 4 0.02666667 0 0.00000
#> 5 0.02666667 0 0.00000
#> 6 0.03333333 0 17.68707
#> 7 0.04000000 0 17.86942
#> 8 0.04000000 0 0.00000
#> 9 0.04000000 0 0.00000
#> 10 0.04000000 0 0.00000